A (Ghost) Fork in the Road: What Can We Expect From Senga’s Premier Pitch?

It’s been a tough start to the season for the Mets’ rotation. Their two-headed ace monster isn’t looking so fearsome, as Justin Verlander went on the IL before throwing a regular-season pitch — joining fellow free-agent signee Jose Quintana — and Max Scherzer has been ineffective through two starts. To make matters worse, Carlos Carrasco dealt with erratic velocity in the first of the team’s back-to-back blowout losses at the hands of the Brewers and yielded a six-spot against the light-hitting Marlins. But one major bright spot has shone.
Kodai Senga, the former three-time NPB All-Star, shut down the Marlins in his Mets debut. With a trademark offering he calls the “ghost fork” and an emblazoned glove to match, he seems poised to become a fan favorite.
Kodai Senga's ghost fork glove ? pic.twitter.com/0Xr9zaL8l7
— David Adler (@_dadler) April 2, 2023
Senga turned to his bread and butter 26 times in his first start, and it generated nine whiffs on 14 swings despite just a 27% zone rate. Every one of his eight Ks came on the fork:
Senga stymied the Marlins again in his second start Saturday. The ghost fork wasn’t quite as dominant but it was still solid, generating three whiffs on six swings across 16 total offerings. Naturally, it won’t net a 34.6% swinging strike rate in every start, but it has certainly looked like a major league out-pitch.
But what exactly can we expect from it going forward? And is it really worthy of its unique moniker?
To begin with, consider the following plot. Each dot represents a single pitch type belonging to a single pitcher (min. 100 tosses). I limited my sample to right-handers for the sake of Senga comparisons — the ghost fork is also included in the chart, circled in red, despite the smaller sample. Movement is spin-induced, without gravity, and from the catcher’s perspective:
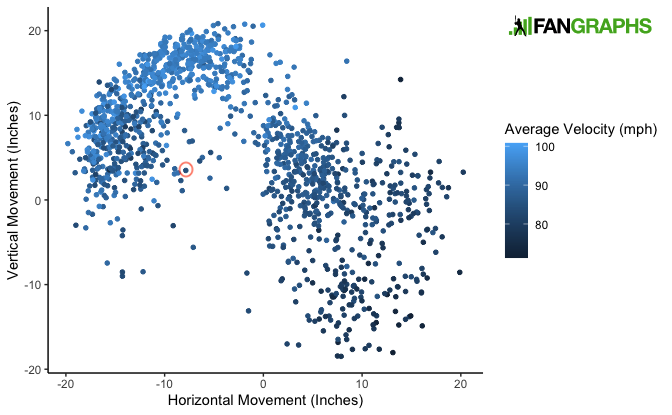
This graph closely resembles one that Eno Sarris published on this site several years ago, in an article entitled “Let’s Invent a New Pitch” — specifically, it looks like his graph that sorts by frequency. Basically, above the ghost fork, there’s a large cluster of fastballs, some that run more and some that rise more than others. To the left of the GF are a bunch of changeups; to the right, cutters and sliders; and down and to the right, curveballs.
Eno pointed out that there was a conspicuous absence of pitches in the lower left quadrant: pitches that drop like curves and run like changeups. The GF isn’t quite in that space, but it’s approaching a different sort of gap left by a lack of pitches that drop like really good changeups but don’t run as much. It’s also thrown harder than some of those changeups.
Yet, it’s not alone. While the GF has 7.9 inches of run on average and 3.5 inches of rise, Luis García throws a splitter that runs 9.0 inches and rises 3.7. James Kaprielian throws a changeup that runs 8.4 inches and rises 2.3. Heck, even Senga’s teammate Carrasco throws a change that runs 8.2 inches and rises 1.1.
Movement isn’t the only characteristic that we should be interested in here, though. The GF also averages 84.4 mph and 1,046.8 rpm, and has a spin axis of 246.1 degrees. García’s split is significantly harder at 88.8 mph and has more run due to a spin axis of 223.8 degrees. Kaprielian and Carrasco’s changeups spin a good deal more at 1,364.7 and 1,307.7 rpm, respectively, leading to more drop but perhaps less deception.
What we really need to do here is use math to determine which pitches are most like the GF. I opted to use Euclidean distance, which the folks over at BaseballCloud have utilized to examine pitch similarity before. Basically, Euclidean distance is what you used in middle school algebra to find the distance between two coordinate pairs: if you consider the line connecting the pairs to be the hypotenuse of a triangle, you can determine the length of that segment using the Pythagorean theorem. Euclidean distance can also be computed for vectors of more than two variables, as long as they are all on the same scale — normalizing average pitch speeds, spin rates, spin axes, and horizontal and vertical movements did the trick here.
I considered a few different ways to think about uniqueness using Euclidean distance. First, I tried sorting by minimum ED, in order to find the pitches with the most dissimilar closest match. But in some cases, very distinct pitches were two of a kind — these weren’t rated as particularly unique by this method. I also tried sorting by mean ED, but this overvalued changeups and curveballs, which were at the far ends of the plot above.
Ultimately, I combined these strategies and settled on taking the mean ED of the five closest matches. This way, even if very distinct pitches were two of a kind, the distance of their four other closest matches would bear out their uniqueness. Further, this didn’t overvalue changeups and curveballs; their uniqueness numbers weren’t overstated due to the inclusion of comparisons to pitches on the opposite side of the plot.
The pitch that stood out the most in this regard was Logan Webb’s changeup. The way Webb throws his change adds 5.6 inches of drop on average, whereas pitchers typically added 6.0 inches of ride to their changeups in the dataset. Webb also induces below-average run (7.1 inches compared to the 14.3 average) at around average velo (86.4 vs. 86.2 mph). In other words, it hits the sweet spot that the ghost fork is leaning towards, the blank space on the graph that a pitch can only get to if it sinks like an excellent change but doesn’t run as much. It drops off a table here, fooling Yasmani Grandal:
Next was Tyler Rogers‘ fastball, which makes sense given his unique release point:
His four-seamer induces way less run, is over 10 mph slower, and induces more drop than you’d think. Rogers’ slider, meanwhile, came in third:
Weirdly, his slider has above-average carry, the opposite of his four-seamer.
Ranking fourth was another riding pitch, Kenley Jansen’s cutter. Jansen’s cut-fastball, which averaged 92.2 mph last year, induces more rise than the average four-seamer and more horizontal movement than the average slider. It’s no wonder he’s turned to it at least 58% of the time every season besides his debut en route to becoming the seventh-most successful reliever of all time by WAR:
Nothing else stood out nearly as much as these four offerings, including the ghost fork. However, the GF still graded out well in aggregate, placing as the 92nd-most distinct among the 1,325 pitches in the dataset (really 1,324, because I left out Hanser Alberto’s fastball, as his was the only position-player pitch to eke in).
What bearing does this have on the pitch’s success going forward? Before we get to that question, let’s check out the GF’s closest comps, because among them were three pitches with swinging strike rates north of 20% and two more in the high teens:
| h_mov | v_mov | mph | rpm | Spin Axis | SwStr% | CStr% | Eu. Distance | |
|---|---|---|---|---|---|---|---|---|
| Kodai Senga FO | -7.9 | 3.5 | 84.4 | 1046.8 | 246.1 | 28.6 | 2.4 | — |
| Luis García FS | -9.0 | 3.7 | 88.8 | 1097.9 | 223.8 | 16.8 | 4.8 | 1.6 |
| James Kaprielian CH | -8.4 | 2.3 | 85.2 | 1364.7 | 240.8 | 11.7 | 10.8 | 2.0 |
| Hirokazu Sawamura FS | -8.6 | 3.2 | 92.0 | 1417.6 | 218.8 | 17.8 | 9.9 | 2.0 |
| Mark Leiter Jr. CH | -6.4 | 4.6 | 84.2 | 818.1 | 229.7 | 29.0 | 3.3 | 2.4 |
| Jakob Junis CH | -9.8 | 4.7 | 84.7 | 1394.8 | 228.5 | 6.9 | 10.4 | 3.0 |
| Yu Darvish FS | -6.2 | 5.0 | 89.2 | 1308.8 | 212.2 | 20.3 | 5.0 | 3.2 |
| Shohei Ohtani FS | -5.4 | 2.6 | 89.3 | 1269.9 | 236.9 | 24.4 | 3.5 | 3.4 |
These are some excellent pitches, and pitchers, to emulate. Sneakily the best offering of the bunch, Mark Leiter Jr.’s split-change, is the fourth-most similar to the GF. On 245 changeups last year, Leiter generated 71 whiffs, good for a 29.0% rate. This ranked fourth in the dataset of 1,324 pitchers. Refresh your mental image of the fork with the clip from above and then have a gander at Leiter’s bread and butter:
Brice Turang looked just as silly here as any of a number of Marlins did against Senga.
Now that we’ve marveled at the comps, let’s take a deeper look at the swinging strike numbers among them. In a multiple linear regression, I found that pitchers with larger mean-of-closest-five Euclidean distances had significantly higher swinging-strike and called-strike rates. These results withstood controls for zone rate as well.
At the same time, as you may have noticed in the table above, the majority of the GF’s closest comps were splitters, the whiffiest pitches. The rest, with the exception of Junis’ piece, were pretty whiffy changeups. So, I redid my analysis looking only at changeups and splitters; there were 189 of them that pitchers threw at least 100 times last year. Splitters and changeups with higher mean-of-closest-five Euclidean distances also generated significantly more swinging strikes, though not more called strikes. A lot of these pitches, like Senga’s, aren’t meant to freeze hitters in the zone (the GF has had a 21.4% zone rate so far); they’re supposed to get them to chase. And the more distinct ones tend to get that job done better.
In fact, the kind of splitters and changeups that did garner more called strikes (even with a zone-rate control) were on average those most dissimilar from the ghost fork (i.e., were farther from the GF according to ED):
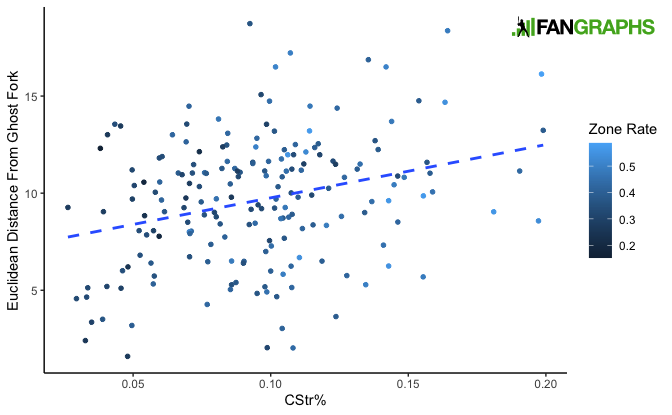
After all, the ghost fork itself didn’t net a single called strike in its debut. But it did induce a lot of whiffs, and swinging strike rate had a negative (though not statistically significant) relationship to GF distance here. Strangely, for pitches that weren’t changeups or splitters, larger differences from the GF portended higher swinging strike rates:
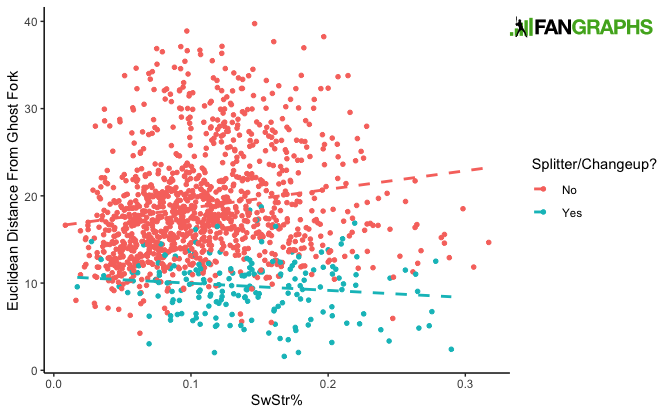
This is most likely because, once you remove all of the changeups and splits, the closest pitches to the ghost fork are sinkers and four-seamers. Then, as you move further away, you reach the whiffier sliders, cutters, and curves.
Let’s summarize what we’ve learned and already knew about splitters and uniqueness. If you can throw a splitter even decently well, you can probably use it to get swinging strikes. If you throw a unique splitter, especially in terms of mean-of-closest-five Euclidean distances, you’re likely to get even more swinging strikes. Lastly, if your splitter is Senga-like, you might get fewer called strikes and more swinging strikes, which is really ideal because these are chase pitches.
Now, let’s summarize what we’ve learned about the ghost fork. The ghost fork is most similar to a splitter, but it’s also pretty distinct, especially in terms of mean-of-closest-five Euclidean distances. It’s also the most Senga-like because, well, Senga throws it. Not to mention, its closest comps include some really good pitches. Thus, I expect it to be successful going forward, though probably not to the tune of the 34.6% swinging strike rate it had in its debut — that’s absurd. But it could definitely hang out in the 20s. Mets fans: it’s been a difficult start to the season, but hopefully you can rest a little easier knowing that so far, the Senga experiment has been a rousing success.
Alex is a FanGraphs contributor. His work has also appeared at Pinstripe Alley, Pitcher List, and Sports Info Solutions. He is especially interested in how and why players make decisions, something he struggles with in daily life. You can find him on Twitter @Mind_OverBatter.

It seems like another thing that stands out about this pitch is how variable its movement is. In the highlight reel from his first start, Senga seems to have thrown Ghost Forks that range from dropping glove-side like a slider, to straight down, to arm side like a change up. This wouldn’t be captured in mean movement, but could be in its range of movement. And I can imagine it will be a pain for batters even once they’re able to identify it or even if they know it’s coming because they still won’t know where it’s going.
I noticed that too. That’s a bit of a different kind of data project; you’d have to take same-size samples for each pitch in order to compare movement variability. Could be one I undertake once we see a sufficient number of ghost forks!
Too bad we don’t have this level of data for Wakefield or Dickey.
The knuckleball is unique and the men who threw the pitch had very little control of it other than to send it in the general direction of home plate.