Converting GO/AO to GB%
Because pitcher ground-ball percentages (GB%) are available at FanGraphs and because they strip away the influence of the defense behind a pitcher, they are (to the best of this author’s knowledge) the best available means of adjudging a pitcher’s ground-ball “profile.”
That said, ground-out/air-out ratios (GO/AO) are still more widely available than pure ground-ball percentages — and are, for example, the only grounder-related number Major League Baseball publishes at its site. So it’s not entirely out of the realm of possibility that one could find himself in such a situation as he had access to the one (i.e. GO/AOs) and not the other (GB%s)*.
*In press boxes, for example, stat sheets featuring GO/AO — but NOT GB% — are frequently available.
With a view towards learning more about the relationship between the two metrics, I found both the GB% and GO/AO for the 90 or so pitchers from 2010 with at least 162 innings pitched. Plotting the two against each other (and using a logarithmic best-fit) we get the following:
That’s pretty impressive, it seems, so far as correlation goes.
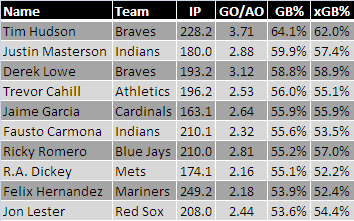
Using the equation you see there, I computed the expected ground-ball percentages (xGB%) for our 90 qualified pitchers using just their GO/AO ratio.
Here are the leaders:
And here are the laggards:
The expected and actual figures are close enough for this author’s liking — and the fact that the equation mostly holds up in the extremes is satisfying.
Finally, for the sake of reference, here’s a table with approximate equivalencies for GO/AO and GB%:
Note that these equivalencies only hold — so far as I know — for major-league pitchers. That Chris Balcom-Miller, for example, posted a 2.13 GO/AO in 108.2 IP at Low-A Asheville last season does not necessarily mean that he induced grounders on 52% of balls in play. (It should be noted, however, that Chris Balcom-Miller is a future star and you would do well to draft him for your fantasy team or whatever this very second.)
Carson Cistulli has published a book of aphorisms called Spirited Ejaculations of a New Enthusiast.




Carson, a groundout to airout ratio means:
g/a
A groundball percentage means:
g/(g+a)
So, in order to convert a ratio into a percentage, you do:
ratio/(ratio+1)
A g/a of .5 means a gb% of 0.33. A g/a of 2 means a gb% of 0.67, and so on.
However, in MLB, they include lineouts from the numerator and denomiator in the g/o ratio. But, they are included in the gb%. So, a gb% is actually:
g / (g + a + l)
Furthermore, in g/a refers only to outs, while gb% refers to all contacted balls. So, you’d have to convert the go to a gb by saying doing go/.75 = gb. And so on.
***
All to say: I don’t doubt the best-fit of the equation you found.
I do think that we can come up with a different equation that is grounded (no pun intended) in logic. And you can then do a best-fit against that equation.
include = exclude
What he did is fine wrt theory. GO/AO is an odds ration, when he takes the log, he then has a log odds ration. This is typically the response in an logit. Now, he puts it on the independent side, but hey.
The main change this suggests is in the error model, but with such high counts, it won’t matter, GB% is binomial which converges to normal in the region these pitchers are in.
Right.
If you have a g/a ratio of .500, 1, 2 the ln of that is going to give you: -.69, 0, +.69. So, perfectly symmetrical. Which matches what the g/(g+a) would give you of .333, .500, .667, respectively.
But, the actual equation for gb% is g/(g+a+l). Would the ln(g/a) still necessarily hold as a core part of the conversion?
I don’t know, I’m asking.
Tango, it’s G/A, not G/F. LD should be included in AO.
Following up:
To convert the ratio to a rate, if we had the exact same parameters in both, we’d do:
g% = g/(g+a) = .x*ln(g/a) + .5
That x would approach 0.25 as g/a approaches 1. And in MLB, x would range from .24 to .25.
So, if we used all contacted balls, then a best-fit equation would come in at something like .25*ln(g/a) + .5.
But, as noted, the ratio actually uses only outs, and excludes lineouts. The rate uses all contacted balls.
Carson’s best-fit, using observed data, changes that .25 coefficient to .18. It changes the intercept from .5 to .38.
My question is if someone here would like to try to come up with an equation without relying on individual data, and simply use some logic to the process. To presume that 20% of batted balls are line drives, that 25% of those are lineouts, and so on.
I don’t understand where “That x would approach 0.25 as g/a approaches 1. And in MLB, x would range from .24 to .25.” comes from.
I think the more interesting thing to do would be to show that of the residual, some of it is explained by, i.e. the UZR of the players (obviously infield UZR should move a point to the right and outfield UZR should move it to the left.)
You can rewrite GB% as:
GO + GB_H /(GO + GB_H + AO + A_H)
Where GB_H is ground ball hits and A_H is air ball hits.
GO+AO is going to cover something like 60% of all BIP. You could, if you wanted to get clever, do this instead:
GO + GB_H /(GO + GB_H + AO + HR + A_H_BIP)
So now you only have to worry about estimating GB_H and A_H_BIP. The question then becomes how well we trust the estimate of GB_H and A_H-BIP given to us by the batted ball stringers.
I think this would be the basic point, right? That we’d estimate GB_H and A_H based on GB_O and A_O.
Basically, taking the factual information of g/a ratio of outs only and translate that in a simple equation into a g/(g+a) rate of contacted balls. So, if you see someone with a 1:1 g/a out ratio, you can then say that’s a GB contacted rate of 38.3%.
I’m entirely prepared to bow to your wisdom. Let there be no mistaking.
Two questions:
1. MLB really excludes lineouts? Isn’t that a bizarre choice? It seems to me as though the advantage of GO/AO is that you can bucket all GB outs on the one hand and all line outs and fly outs in the other, and that way classification becomes less of a problem.
2. My main concern here, as you might guess, is just having a quick-reference sheet, so to speak. Even if the process I’ve used ISN’T the most logical way of getting to the answer, it still “works,” yes, as a quick reference?
3. Pun not intended AT ALL? Not even, like, 10%?
Colin is saying lineouts are included. I agree with you that it would be highly bizarre to exclude them.
I agree with you that your equation does the job, and for that, it’s good. I was more asking as a technical exercise, that instead of relying on sample data, can we get to the same place without the individual player data, and just use league-wide data.
Pun: no, not at all. I was just writing, and then I stopped when I realized what I said.
Tango’s mistaken, I think – AO should include fly balls, line drives and popups.
Lesse here – on MLB.com, Cain is listed with 248 AO. From Retrosheet, I come up with 178 fly ball outs. If I include PU and LD, I get 283…
Hrm. Okay, maybe I’m the one mistaken here.
No, I spotchecked a few player – looks like LD outs are excluded. I concur that it’s extremely odd for them to do so, and I don’t know if that’s been done historically.