Taking A Look At Spin Mirroring, Part 2: Misconceptions and Practical Applications

Back in November, I wrote a piece on spin mirroring in which I broke down the phenomenon and its applications, along with theories on its effectiveness. There have been some misconceptions about how spin mirroring actually works. I’m going to attempt to break down how to create “true” (or parallel) spin mirroring, which is based on much more than just opposite spin directions. Spin direction, spin axis, tunneling, and “seeing” spin are all factors that make up this phenomena.

The premise of the strategy is based on a hitter’s potential to recognize spin and the pitcher having the ability to tunnel two pitches, which can create a repelling effect in terms of opposing Magnus force. This juxtaposing effect can create a large spread ratio between the tunnel point and the position of the pitches when they cross home plate. So long as the spin direction contrast is somewhere between 170 and 190-degrees, and their gyro degrees (where the spin axis is pointed in space) are similar, true spin mirroring can be facilitated.

The below example shows how spin direction and the spin axis of two pitches are affected by the contrary Magnus effect (as well as gravity), which creates the appearance of them almost pushing off from each other. There is no additional force from the balls themselves acting on each other; it’s simply how each pitch, individually, responds to this law of physics:

One thing I want to point out as we dive into this is that the Driveline EDGE tool I’ll be using doesn’t account for gravity, drag, or the effect seam orientation might have on ball flight, as well as any park factors like air pressure. These are provided to add visual context to reinforce my statements. That isn’t to say the tool doesn’t have uses otherwise; it relies more on the movement the pitcher is able to generate by himself, which is elaborated on here.

We’ll start with spin direction. Let’s say you throw a fastball and a curveball, which is the ideal combination for mirroring because fastballs are thrown with backspin and curveballs are thrown with a substantial amount of topspin:

Magnus force “pushes” the fastball up, while the curveball gets “pulled” down, creating a large amount of separation:

The next factor to take into consideration is spin axis. This is how the pitch’s spin direction is actually oriented in three dimensions. To help understand this, the image below shows both the two-dimensional perspective (x and z) on the left, and the three-dimensional (x and y) on the right:

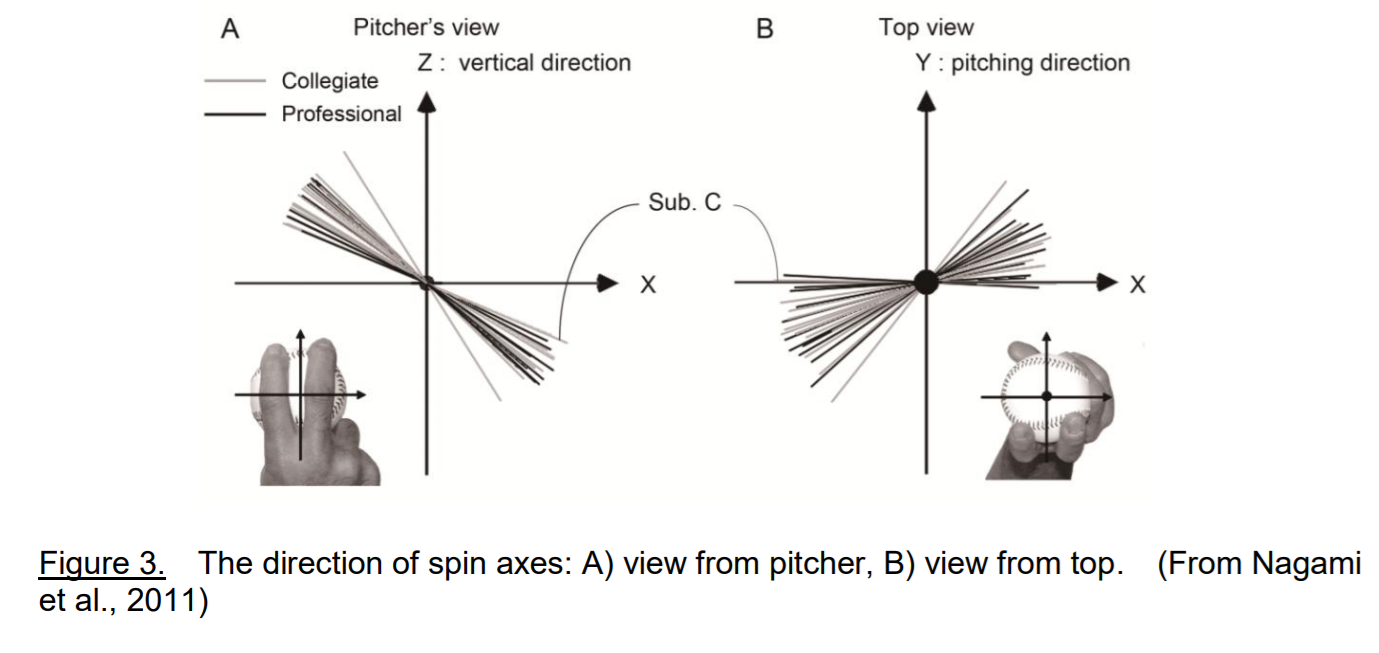
We look at spin direction in two dimensions (A) with an axis (B), regardless of spin direction, that is perfectly parallel to home plate and independent of its actual orientation in space. Have a look at the example below, where two pitches can have the same spin direction, but not look as alike as you may assume by just looking at spin direction alone:

As you can see, they spin the same directionally, but that spin is oriented very differently – either because of how the pitcher is holding the ball, or how they are releasing it in conjunction with their wrist or forearm action.

Now, let’s go one step further and bring the curveball back into the fold. I’ll again put the fastball at a 12:00 spin direction with perfect efficiency, but this time, we’ll degrade the curveball spin efficiency while keeping the spin direction at 6:00:

While there is a small amount of mirrored spin, their gyro orientations aren’t ideal.

So, does that matter? Well, sort of. It matters in the sense that if hitters can pick up on spin, then this combo will be much easier to identify than the perfect mirror example we looked at earlier. If we remove the possibility of seeing spin, and if the two pitches can effectively counteract each other (move in almost perfectly opposite directions) after the tunnel point, it’s not a detriment to the pitcher.

Which brings us to tunneling ability. While there is still some research to be done, all the current studies seem to suggest that the closer together your pitches are at the hitter’s decision point (about 25 feet before home plate), the harder it becomes for hitters to commit. This is why you see hitters hesitate on pitches that land for strikes or take terrible swings at a pitch that was outside of the zone. If a hitter gets a 95 mph fastball up in the zone that they take for a strike, the next pitch being a curveball that comes out of the same tunnel might give the illusion (albeit briefly) that it could be the same pitch. The hitter is then put into a fight or flight-type of dilemma, which could result in them swinging wildly, or perhaps watching the pitch fall into the bottom of the zone for another strike.

We saw the effect of tight release points on ideal mirroring earlier, but keep in mind that’s a perfect situation that doesn’t regularly exist. Here’s a more average situation, with a few inches of additional separation (2.2 inches is league average). You can see the movement patterns are fairly different, even though I’ve changed this example to a 3/4 arm slot, for which I’ve accounted by making a one-hour spin direction adjustment for each pitch:

Can a hitter differentiate each pitch in this example? Maybe, but it varies from player to player; some might pick it up on it right away while others are just as lost as they were had they faced the earlier fastball/curveball example. Also consider that just because a batter knows what pitch is coming, it doesn’t always follow that their decision to swing (or not) will result in a successful outcome.

Finally, we come to the notion of “seeing” spin. Have a look at this video where I show both topspin and backspin (thanks to Barton Smith for the original clips):

The first shot shows both back and topspin from the same perspective. Could you tell the difference? In the second part of the clip, I separate both pitches. Is it any easier? Keep in mind, the spin is much slower than game speed. And if you were able to see the spin, all you’d be able to notice are the vertical lines near the outside of the baseball. Even if your eyes are good enough to see that, imagine trying to tell which one is spinning which way.

You can see that if a pitch has a disparity of even 10-degrees, it might tip the pitcher’s hand, should a hitter recognize the difference.

Let’s apply this to a real-world situation.

We will use Detroit Tigers relief pitcher David McKay as our example, as he presents an ideal tinkering subject due to pitches with high spin efficiency with workable spin directions that contrast at around 160-degrees. In conjunction with his elite spin efficiency (98.8%), McKay also has a Bauer Unit score of 25.4, which encourages his fastball to stay up in the zone:

McKay throws a fastball (more than likely a two-seamer/sinker) and a curveball. According to his 2019 pitch data, his fastball was thrown with a spin direction of 1:20 with 99% spin efficiency. His curveball was thrown at 8:00 with a 97% spin efficiency. Here is what his combo looks like using this data along with his actual release points:

The spin is really close, but his release points might tip a hitter off. We are talking about a matter of a few inches, but sometimes that’s all a hitter needs to pick up on in situations like this.

So what should McKay do to rectify this encumbrance? Well for one, both axis orientations are fine. His spin direction doesn’t necessarily need to be changed, but it might be necessary considering the arm slots for each are a bit different. In this case, I’d suggest changing the fastball a bit. It’s released higher than his curveball, and given the heavy sidespin component of the curve, there isn’t any risk lowering the fastball arm slot; there won’t be much “hop” over the fastball, which would need to be accounted as it might otherwise “break” the tunnel early. If the “hop” were present, it would be advisable to work on the curveball instead.

In any case, if McKay can drop his arm slot by maybe four inches squared, it would be more in line with the curveball. This can be accomplished by lowering his arm, or by working on adding a small amount of lateral trunk tilt to make up the difference. However, if McKay has a high level of comfort with his mechanics, a change may not be advisable so long as he’s getting good results from both pitches.

Having taken these several factors into consideration, the ideal of true spin mirroring should become a bit clearer. Just having opposing spin directions isn’t enough. One simple way to determine the true mirroring effect is by inspecting spin efficiencies, which alludes to the amount of gyro a fastball and curveball possesses. If you have comparably high spin efficiencies for both, the odds are good that they are candidates for mirroring.

Even if you come across a pitcher with the blueprint for this plan of attack, there are other tools that need to be utilized. Each axis orientation in space, along with a solid tunneling foundation, can help capitalize on a hitter’s ability to potentially recognize spin while creating the kind of separation at the commit point that can make a hitter look really foolish.