Daddy Hacks or: The Lone Peril of Swinging Too Hard

Hi! It has been made to clear to me that my use of f = m * a as a narrative device herein was quite distracting, chiefly because in this context it’s incorrect. I apologize in advance to renowned baseball physicist Prof. Alan Nathan, should he ever read this; to all other physics enthusiasts who have remarked on the mistake; and to me, for embarrassing me. Ideally you will see past it and appreciate the meat and potatoes of the post for what they are: that there is possibly declining marginal utility to bat acceleration in a way we don’t seem to witness for bat speed. Thanks, and sorry again!
I can’t possibly begin to cover all the excellent work concerning Statcast’s new bat tracking data. Now as much as ever, it’s important to support your local Baseball Prospectuses, PitcherLists, Baseball Americas, FanGraphses and freelance Substack writers. We move quickly in these parts. There’s so much analysis to consume, all of it superb.
When confronted with this new data, one of my first instincts was to see which metrics from other areas of sabermetric analysis could be replicated within the bat tracking framework. Enter 90th-percentile exit velocity (90EV); it’s a powerful shorthand metric that distills a lot of information about the top end of a hitter’s exit velocity distribution into a single number. It’s not perfect, and other metrics outperform it, but it’s easy to see how it has become popular in contemporary analysis, especially in prospecting and scouting circles.
So I looked to 90EV for inspiration with respect to bat speed. I assumed bat speed, being a primary input to exit velocity, would exhibit similar strengths in characterizing a hitter’s distribution of bat speeds by consolidating the most crucial speeds into a single value. Indeed, parsing bat speeds into deciles appears to work really well:
| Bat Speed Decile | Avg EV | Contact% | Barrel% | Square Up% | Blast% | xwOBAcon |
|---|---|---|---|---|---|---|
| 0th up to 10th | 71.2 | 65.4% | 0.1% | 36.3% | 4.3% | .130 |
| 10th up to 20th | 77.2 | 78.2% | 1.3% | 39.5% | 8.5% | .191 |
| 20th up to 30th | 78.9 | 78.9% | 2.9% | 36.9% | 11.5% | .232 |
| 30th up to 40th | 80.5 | 79.2% | 3.5% | 36.5% | 13.4% | .256 |
| 40th up to 50th | 82.1 | 78.8% | 5.5% | 37.2% | 16.0% | .284 |
| 50th up to 60th | 83.3 | 79.3% | 7.2% | 37.4% | 18.5% | .307 |
| 60th up to 70th | 84.6 | 78.1% | 8.3% | 38.6% | 20.1% | .322 |
| 70th up to 80th | 86.2 | 78.0% | 12.1% | 39.6% | 23.3% | .369 |
| 80th up to 90th | 87.7 | 77.6% | 11.9% | 40.9% | 25.3% | .377 |
| 90th through 100th | 88.5 | 82.3% | 13.8% | 40.4% | 29.2% | .404 |
Average exit velocity increases linearly with bat speed. So does contact quality (xwOBA on contact, or xwOBAcon) and barrel rate (Barrel%). All of these trends meet expectations. What defies expectations, however, is that contact rate (Contact%) spikes for a hitter’s top 10% of bat speeds. Whereas bat speed correlates positively with whiffs (that is, more bat speed typically means more whiffs), the average hitter’s fastest swings evidently produce more contact, not less, and by a substantial margin to boot. That’s an amazing collective feat. It’s like the numeric equivalent of “seeing beach balls.”
There’s more to this than meets the eye. Why is this possible? Let’s view the predicament through the lens of physics. Do you remember physics? One thing I remember — in addition to spending an inordinate amount of time across several days with my friend Kevin trying to bounce an empty plastic apple juice bottle on its side to get it to land upside-down on its cap — is that force equals mass times acceleration. Not velocity, but acceleration. The typical swing starts at an initial velocity of zero and makes contact at a final instantaneous velocity of X (in this case, “Bat Speed”). To reach X mph from 0 mph, the bat must accelerate. How much the bat accelerates determines how much force the hitter imparts upon the ball. And what is a hitter’s primary job if not to impart force upon an unsuspecting, unassuming baseball?
The bat tracking data from Statcast does not include mass (i.e., the weight of the bat), and we barely have acceleration. At best, we must make a flawed assumption that bat acceleration is constant throughout a hitter’s swing. (We make the same assumption for a pitch’s movement through space — how bad could it be? Maybe don’t answer that question.) I cobbled together some crude acceleration estimates based on bat speed and swing length using my extremely time-withered recounting of 11th-grade physics as a Martinelli’s bottle tumbled through my brain. Villain origin story aside, what relevance is acceleration if we have final speed? Namely, we can use acceleration to diagnose differences in seemingly identical bat speeds. Consider two swings with bat speeds of exactly 75 mph, yet one swing is only seven feet long, the other eight feet. We can assume the former swing had to accelerate more quickly across a smaller distance to reach the same instantaneous velocity on contact as the latter.
So instead, how do a hitter’s bat acceleration deciles correspond with various measures of production? Much differently:
| Bat Acceleration Decile | Avg EV | Contact% | Barrel% | Square Up% | Blast% | xwOBAcon |
|---|---|---|---|---|---|---|
| 0th up to 10th | 68.8 | 52.9% | 0.3% | 25.5% | 3.5% | .112 |
| 10th up to 20th | 76.2 | 67.0% | 1.7% | 31.8% | 7.6% | .177 |
| 20th up to 30th | 79.2 | 76.2% | 3.3% | 37.3% | 12.1% | .232 |
| 30th up to 40th | 81.1 | 81.2% | 5.2% | 40.5% | 15.7% | .277 |
| 40th up to 50th | 82.8 | 84.3% | 6.8% | 42.8% | 19.3% | .311 |
| 50th up to 60th | 83.9 | 84.3% | 8.9% | 42.7% | 20.5% | .333 |
| 60th up to 70th | 85.1 | 85.3% | 9.3% | 44.8% | 23.2% | .351 |
| 70th up to 80th | 85.7 | 84.5% | 10.2% | 43.4% | 23.3% | .363 |
| 80th up to 90th | 86.4 | 80.9% | 11.0% | 40.2% | 23.0% | .368 |
| 90th through 100th | 86.4 | 79.6% | 10.3% | 34.9% | 22.2% | .350 |
In moving from the penultimate decile to the top decile, the league-average exit velocity plateaus at 86.4 mph (rather than continuing to increase linearly). Contact rates peak closer to somewhere between the 60th and 70th percentiles, as does Statcast’s new square-up percentage (Square-Up%). Barrels peak below the 90th percentile, as does Statcast’s new Blast rate metric (Blast%), as well as our tried-and-true xwOBAcon. The texture of assessing swing efficacy (through the viewpoint of a single bat tracking measurement) has changed entirely.
All of which is to say that daddy hacks — true swing-out-of-your-shoes daddy hacks — perhaps aren’t the best way for a hitter to optimize his offensive production. Which isn’t to say that daddy hacks aren’t good, productive swings — they are still among the most productive swings a hitter can make, and a hitter ought to err on the side of too much acceleration rather than not enough — but this is a question of optimization, not magnitude.
What, then, is the best way to optimize? What’s the ideal combination of bat speed and bat acceleration, using this unsophisticated percentile framework? It’s somewhere in the red-highlighted area below, which is typically not where a hitter maximizes his acceleration:
| Acceleration → ↓ Speed |
0th-10th | 10th-20th | 20th-30th | 30th-40th | 40th-50th | 50th-60th | 60th-70th | 70th-80th | 80th-90th | 90th-100th |
|---|---|---|---|---|---|---|---|---|---|---|
| 0th up to 10th | .113 | .187 | .166 | .160 | .143 | .129 | .083 | .076 | .000 | .123 |
| 10th up to 20th | .121 | .223 | .239 | .233 | .202 | .188 | .172 | .131 | .083 | .051 |
| 20th up to 30th | .095 | .184 | .283 | .298 | .288 | .238 | .261 | .224 | .158 | .071 |
| 30th up to 40th | .060 | .150 | .264 | .312 | .336 | .286 | .286 | .263 | .207 | .113 |
| 40th up to 50th | .004 | .119 | .246 | .320 | .341 | .352 | .348 | .297 | .255 | .144 |
| 50th up to 60th | .012 | .099 | .216 | .324 | .355 | .347 | .363 | .333 | .285 | .242 |
| 60th up to 70th | .000 | .057 | .134 | .272 | .364 | .382 | .358 | .354 | .347 | .234 |
| 70th up to 80th | .000 | .119 | .116 | .233 | .323 | .401 | .413 | .436 | .397 | .336 |
| 80th up to 90th | .000 | .210 | .105 | .108 | .234 | .382 | .386 | .435 | .436 | .360 |
| 90th through 100th | .426 | .000 | .247 | .145 | .216 | .253 | .379 | .402 | .455 | .410 |
It is where he maximizes bat speed, but through a longer swing that allows more time to accelerate (at a slightly lower rate of acceleration) to its maximum speed. That’s not something you can glean from bat speed alone. As such, top-10% bat speed as a 90EV-equivalent metric simply does not capture the information we want it to capture, at least not in its entirety.
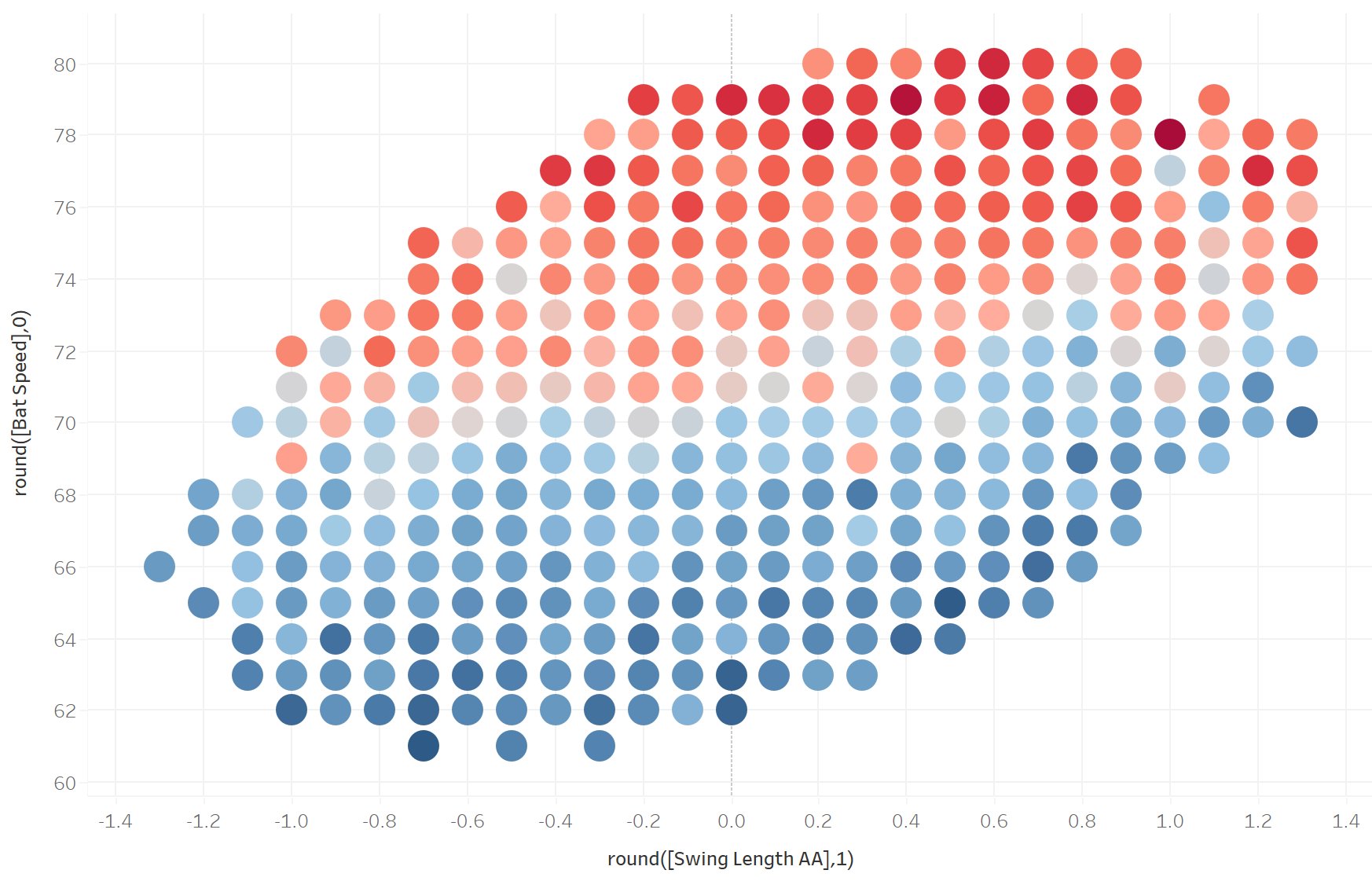
The solution to the problem of optimization vis-à-vis contact quality for any hitter, regardless of size and strength, is to minimize swing length for any given bat speed (red = high average exit velocity, blue = low).
To be clear, long swings aren’t bad; in fact, a longer swing (in distance, not time) tends to denote more distance across which to accelerate, which naturally creates more bat speed. You can actually see that longer swings are associated with higher bat speeds and higher exit velocities. But if a hitter can achieve the same bat speed with a shorter swing, he will inherently generate more acceleration.
Presumably not all hitters take daddy hacks at the same frequency. At the same time, I cannot with any confidence attest to which hitters take more daddy hacks than others. Knowing what we know about them, I doubt Steven Kwan takes anywhere near as many daddy hacks as Javier Báez. This is why I have taken care to refer to league averages and “the typical hitter.” At what threshold above a hitter’s average bat speed do contact rate and quality start to degrade? Does that threshold change from hitter to hitter?
As for daddy hacks themselves, both bat speed and acceleration correlate directly with ball-strike count. Bat speed and acceleration peak when the count is most in their favor (3-0), and decrease steadily as the count becomes less favorable, with hitters’ slowest swings occurring in 0-2 counts. It is in those advantageous counts that hitters possibly do themselves a disservice (just barely a disservice, but a disservice nonetheless) by taking daddy hacks rather than taking a little off it to ensure they square it up a little better — to ensure the chaos is in fact controlled:
| Bat Acceleration Decile | Ahead | Even | Behind | Two Strikes |
|---|---|---|---|---|
| 0th up to 10th | .225 | .221 | .245 | .081 |
| 10th up to 20th | .275 | .257 | .287 | .135 |
| 20th up to 30th | .311 | .305 | .295 | .179 |
| 30th up to 40th | .343 | .344 | .320 | .216 |
| 40th up to 50th | .373 | .359 | .355 | .252 |
| 50th up to 60th | .390 | .395 | .363 | .263 |
| 60th up to 70th | .428 | .393 | .398 | .277 |
| 70th up to 80th | .441 | .407 | .393 | .285 |
| 80th up to 90th | .467 | .433 | .407 | .265 |
| 90th through 100th | .455 | .408 | .348 | .255 |
The very best swings, then, appear to be those that increase bat speed through acceleration rather than swing length, neutral of pitch location. I say “neutral of swing location” because swing length correlates with lateral (east-west) pitch location, with inner-half pull-side approaches yielding longer swings. The red-and-blue jelly bean above shows that swing length is positively correlated with exit velocity, so it makes sense that pull-side swings yield superb results. They not only take advantage of a shorter outfield wall distance but also enable the hitter to generate more bat speed across a longer swing distance. Two swings with identical rates of acceleration will produce different swing lengths and final bat speeds based exclusively on the pitch’s location. This whole thing has been about the swing — it’s primarily about the swing — but it’s about swing decisions, too, and the augmentative powers of those decisions.
Bat speed becomes reliable much more quickly than exit velocity, which on its own should quickly cement it into the analytical toolbox. Like any other metric, though, it still requires an immense amount of context, lest we risk comparing apples to oranges. Acceleration is some of that necessary context, and I anticipate that once we have year-over-year data, we will use it to diagnose injuries or spot signs of decline better than bat speed by itself.
All stats are through May 19.

You are using force incorrectly. For collisions you would want to use a momentum balance (momentum is conserved) which is based on mass and velocity to impart the initial exit velocity onto the ball. The acceleration rate throughout the swing doesnt matter, only the velocity when the ball is hit.
I was going to say the same thing.
One thing that I’d add, though, is that while the acceleration rate doesn’t matter as a relevant boundary condition to the impact itself, this measure of imputed acceleration very well might be a meaningful proxy for certain kinds of swing mechanics or swing decisions. And those could be fruitful paths of study.
But, yeah, you’d definitely rather be hit by a car that just accelerated up to 5 mph than one slamming on their brakes to get down to 30.
Also the units don’t work out to find acceleration anyway. Velocity is measured of units (distance/time) and acceleration is (distance/time^2). To get an average acceleration, the author would need to divide the swing speed by the length of time to complete the swing not the swing length.
Of all the things I articulated incorrectly from a physics standpoint, I did at least do this part correctly. I’m not a total numbskull! But clearly I am not qualified to discuss physics which is why I had never done so until now. And perhaps never again! We’ll see.
I wouldn’t say acceleration is being used by the author incorrectly if we’re examining hitter’s swings. Yes, from the point of impact, all that matters is the momentum transfer during the collision for imparting energy (and recall that Newton’s 2nd Law is more correctly translated as F = dp/dt, not the more commonly used F = ma), but there’s a significant difference in how a batter arrives at that velocity. I’ve been harping on Arraez recently, but I was initially confused by his ranking among the lowest swing speeds when his bat looked so quick through the zone. I’m speculating, but I’d imagine he ranks much higher among swing accelerations which would go along with his ability (and others of his ilk) to watch the ball travel deeper into the zone before pulling the trigger. The swing acceleration gives a more complete view of the totality of the swing rather than the instantaneous velocity snapshot at the end.
edit: above comment went through
Haha although they are absolutely right to lambast my woeful grasp of physics concepts I appreciate you coming to my defense; I think their criticism of my use of f=ma loses the forest for the trees when the reality is acceleration is the difference between identical bat speeds at different swing lengths, or identical swing lengths with different bat speeds. The context it adds is crucial. But it’s ok, I deserve it :”’)
I think the acceleration provides an important distinction: it’s not the velocity, it’s how fast you get there. A long swing full of holes will be impressive only from a swing velocity standpoint, but a more modest swing velocity could be more conducive to better swing outcomes like fewer swing-and-misses, more foul balls, etc.