More Fun With Batted Ball Spin Data

Last week, I wrote an article about the influence of batted ball spin. The takeaways were simple: For one, even though confounding variables like temperature and wind speed are hard to eliminate, it’s entirely plausible that batted ball spin alone can subtract crucial amounts of expected distance. Also, while hitters may display a penchant for certain types of spin, they seemed to have little control over it on a daily basis. Potential inaccuracies aside, these findings made sense; hitting a baseball is hard, and batted ball spin is just another piece of the puzzle.

After the article ran, I didn’t expect to revisit this topic anytime soon. But two things inspired me to start exploring again. First, a Twitter mutual was kind enough to provide me with Trackman data of college baseball games that include — you guessed it — batted ball spin axis, which opened up multiple avenues of research. Second, Dr. Alan Nathan, a physics professor at UIUC, summarized his own findings on batted ball spin in the comments. Armed with new data and knowledge, it was time to dive back in.

Let’s start with a word from Dr. Nathan. This part of his comment struck me as particularly interesting:

“The increased lift with backspin (which increases distance) gets overwhelmed by the increased drag (which decreases distance) once the spin exceeds 2,500–3,000 rpm.”

As well as this:

“…it is very difficult for a ball hit at 25–30 deg to have topspin.”

In demonstrating the impact of batted ball spin, I’d chosen fly balls with a decent amount of exit velocity (95–100 mph) and an ideal launch angle (25–30 degrees), along with an assumption that topspin was the main culprit in slashing distance. But as clarified by Dr. Nathan, such fly balls are devoid of topspin. Rather, the contributing factors are an increased drag and, as he also mentioned, the existence of sidespin that doesn’t aid in lifting the ball. That certainly defied expectations.

Indeed, when I recreated the initial graph of batted ball spin rate against actual minus expected distance using the new data… well, I wasn’t able to! That’s because after applying a topspin-only filter, all the points on the graph vanished without a trace. Not that he needs it, but the disappearance gave credence to what Dr. Nathan had said. The truth is a bit more complicated, however. Here’s a plot showing the distribution of launch angle for each type of spin. It’s not what you might expect:

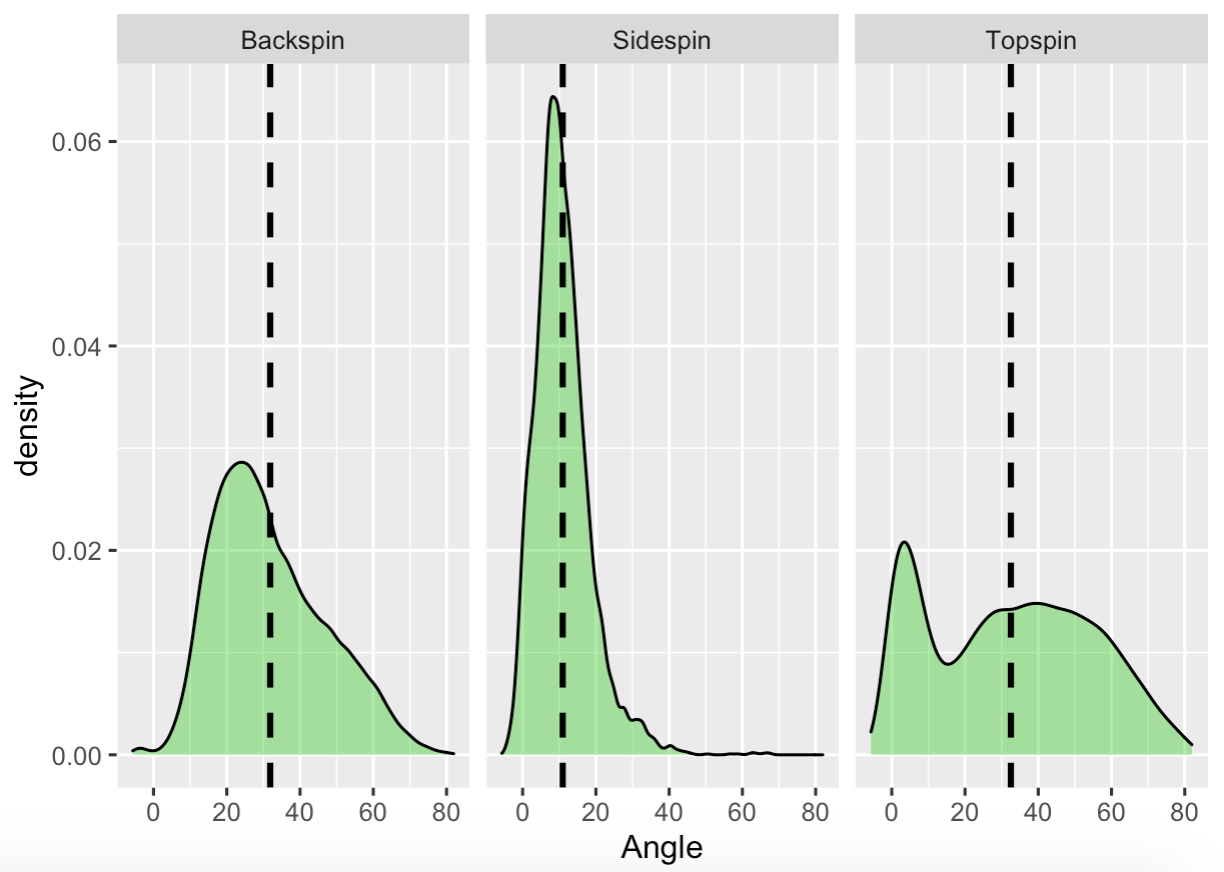
Huh. So top-spinning balls are in fact capable of achieving that 25–30-degree range. The distribution for back-spinning balls makes sense, as backspin is what causes lift. And since sidespin mutes distance, it also makes sense that they average the lowest launch angles, but the extremely narrow distribution is puzzling. Still, the mystery of topspin remains — that is, until we take exit velocity into consideration. Here’s the same graph as before, but with average exit velocity instead of launch angle:

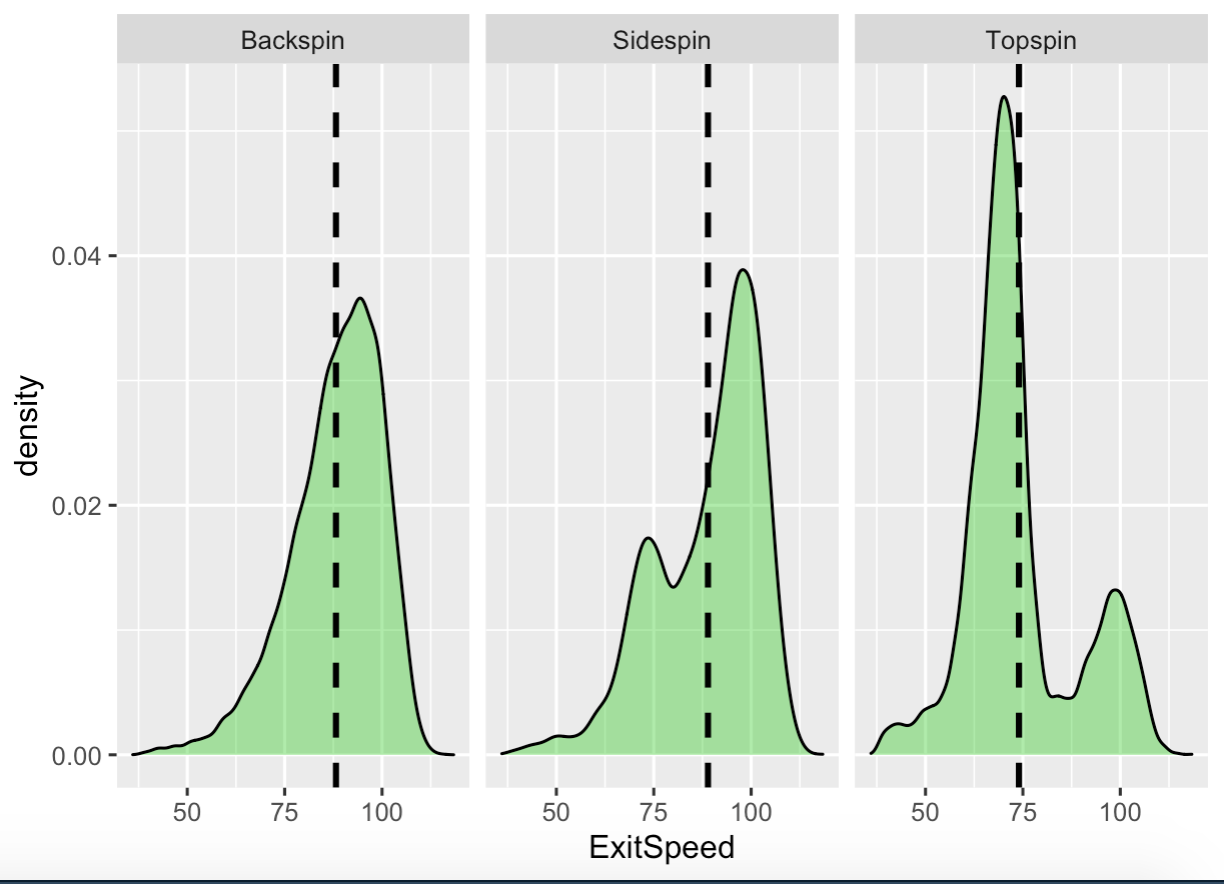
There we go. Save for a slight dip at around the 80-mph mark, balls with sidespin closely resemble those with backspin in terms of exit velocity. But balls with topspin are overwhelmingly driven with only a modicum of power. Now, it is possible for top-spinning balls to achieve the 95–100-mph range, but an educated guess is that our specific combination of exit velocity and launch angle is near-impossible.

Beyond that, a lot of what’s displayed here adds to the confusion. For example, I’m not sure what to make of a sudden spike in exit velocity in the distribution for top-spinning balls, or why topspin, unlike its cousins, seems to be distributed equally among various launch angles. Physics can probably tackle some of those questions, but for now, this is just what I found.

It also doesn’t help that the process of categorizing batted ball spin is imperfect. The basic rundown: In Trackman data, a spin axis of 180 degrees represents perfect backspin; therefore, an axis of zero or 360 degrees — which are functionally the same — represent perfect topspin. Everything in between the poles result in a mixture of either backspin or topspin and sidespin. There had to be hard cutoffs, though, which means that one ball put in the “topspin” group and another put in the “sidespin” group may only differ by a couple of degrees.

Maybe we can amend that. What if we tried to capture the ratio of back/topspin to sidespin in a given batted ball? For example, a ball hit at a 225-degree axis, which is right at the midpoint of pure backspin (180) and sidespin (270), would be assigned a ratio of 0.5. The scale is continuous, with each degree escalating the ratio ever so slightly. But after running the calculations, what followed were several trials and even more errors. Did this “spin ratio” do a better job of accounting for the gap between actual and expected distance? Nope — raw spin rate kicked its butt each time, even after controlling for multiple variables. And at first, spin ratio didn’t seem to help at all in explaining why certain back-spinning balls added more distance compared to others.

In the end, it helped to stick to a place that by now had become home: that narrow range of exit velocity and launch angle, the borderline hard-hit fly balls. Here’s how batted ball spin ratio ended up being incorporated:

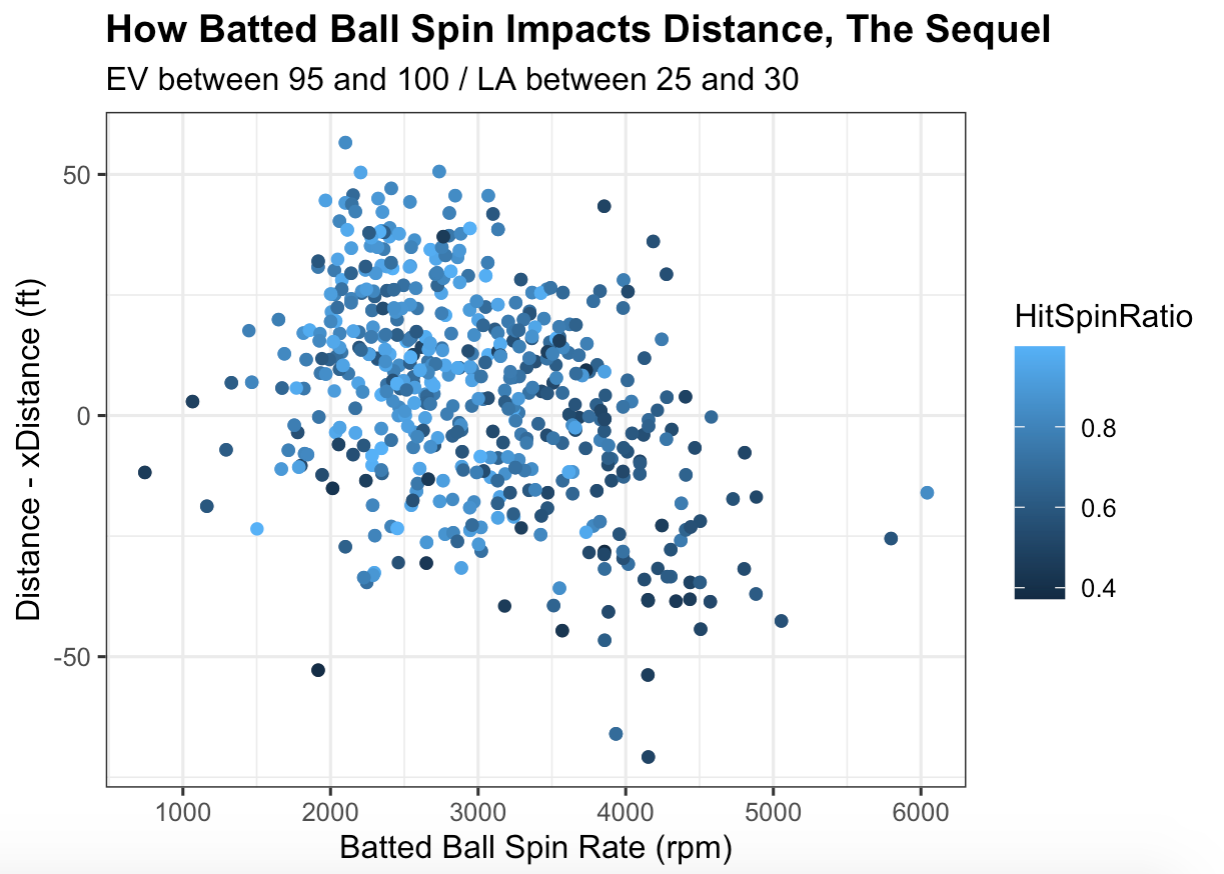
Remember the graph from the previous article? There’s a whole lot more going on in this upgraded version, both in terms of aesthetics and information. While the shades of blue are all over the place, splattered across the gridlines like a Jackson Pollock painting, there’s a general tendency for balls with higher spin ratios (i.e. more backspin) to outperform their expected distances. They also tend to have lower raw spin rates, which once again echoes Dr. Nathan’s comments: The introduction of sidespin disrupts the upward trajectory of a back-spinning ball. But also, this graph is a result of minor adjustments, such as the removal of balls categorized as sidespin, or ones that the Trackman operator deemed as having low-accuracy readings. We ended up with a much stronger correlation between batted ball spin rate and distance differential, which is awesome to see.

If you’ll recall, the previous article also introduced a FanGraphs community post, which assumed balls with more distance than expected must have been hit with backspin, whereas balls with less distance than expected must have been hit with topspin. But we now know that second part isn’t always true. If our favorite subset is any indication, the home runs hitters miss out on can be blamed on the influence of sidepsin rather than topspin, which doesn’t really appear in hard-hit balls. And though too much of it can hurt, the drawbacks of aiming for higher backspin are quite minimal. When I looked at individual college hitters with at least 50 fly balls, how often they imparted backspin had the strongest correlation (r = 0.70) to how much distance they added. That’s irrespective of how much sidespin was present.

In addition, while a sprinkle of sidespin may not help out in the fly ball department, it can certainly boost a hitter’s production on line drives. That narrow-ish hump from earlier representing hard-hit, side-spinning balls is what we’re after. What’s interesting about them is that they tend to fall on the high end of the backspin-sidespin spectrum, which means two things: These balls are getting enough distance to reach the outfield, and, in moderation, they’re adding the hook or fade that’s characteristic of a representative line drive.

Do you who’s really good at achieving a balance between backspin and sidespin? My goodness, that’s Kyle Manzardo’s music! Before slashing .313/.397/.458 in A-ball so far this season, the first baseman absolutely raked in college. And thanks to granular batted ball spin data, we can better understand why that was the case. Below, I’ve plotted every single Manzardo line drive at my disposal, with all the requisite variables:

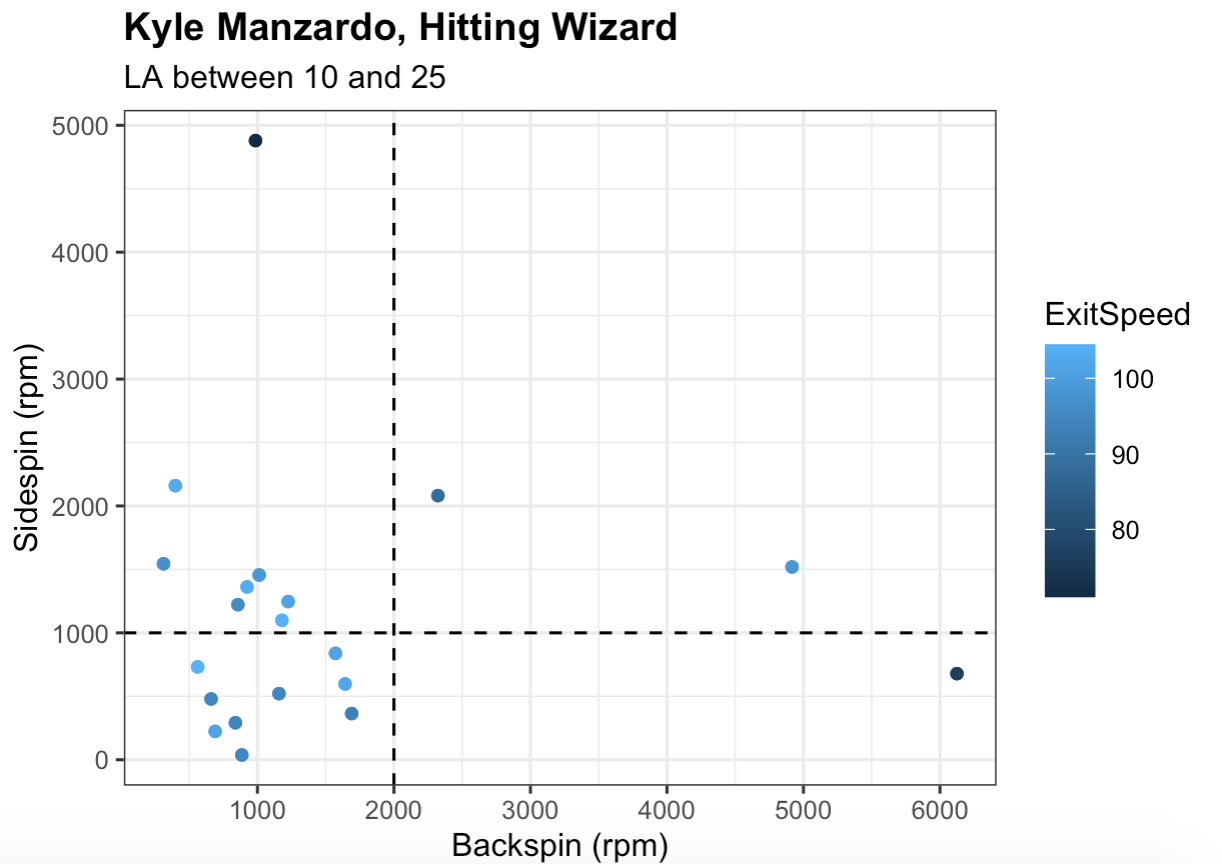
What immediately stands out is how many of his line drives are within or near the bottom-left quadrant, as established by the dotted lines. Consider how most of them came off the bat with more backspin than topspin, but not by a lot, and that their total raw spin rates aren’t overwhelming. It’s hard to pinpoint exactly what combination of spin type and amount maximizes results, but Manzardo’s clockwork regularity seems like a darn good approximation. Above all, check out those exit velocities; rarely did he fall short of the 90-mph mark, a feat that’s likely aided by his ability to generate backspin in the first place. Maybe it’s not so strange that the Rays, a model-driven organization, used their second-round pick on a prospect with little positional value and seemingly minimal pop to compensate. Manzardo may never reach 20 home runs in a season, but if he continues to smoke line drive after line drive, he won’t have to.

One final note: Even after accounting for which type of spin a hitter produced, the day-to-day fluctuations in batted ball spin persist. I’ll wrap things up here, though, because there are way more questions worth asking than I could possibly fit into a single article. Batted ball spin isn’t mainstream right now, mostly because the data isn’t public, but it might be within a few years. We already know hitters are generally either groundball or fly ball hitters, and that some of them are better at getting the most out of their batted ball than others. The million dollar question, then, is how. Which hitters’ achievements lie beyond the realm of exit velocity and launch angle, and what processes have led to them? For that, perhaps we’ll need a new spin — a batted ball spin, that is.

Author’s Note: You can read Dr. Nathan’s excellent research on fly ball carry here.