Triple-Slash Line Conundrum: Voros McCracken Edition

Every few years, the same old question sets the internet aflame: Why do Americans care so much about the British royal family Does batting average matter? If you haven’t seen my favorite formulation of the problem, here’s Tom Tango’s version of it:
Which is the more productive batter (all other things equal)
A.
.315 batting average
.365 OBP
.510 SLGB.
.260 batting average
.365 OBP
.510 SLG— Tangotiger ? (@tangotiger) January 9, 2023
I’ve taken a crack at this exact question before. The answer simply isn’t very surprising. If two hitters have the same on-base percentage and the same slugging percentage, they’re similarly valuable to their team’s offense. That’s why OPS is a popular offensive statistic despite its relative lack of precision; it does a lot of the same work as wOBA and wRC+ because its two component stats are mostly found in similar ratios and correlate well to offensive production. Linear weights are still better, because they do a better job of accounting for how important each plate appearance outcome is when it comes to run scoring, but you can get most of the way there with OBP and SLG.
There’s not much reason to go through the exact math of how wOBA works again, because the people who would be swayed by that math have already been swayed. But sabermetric forefather Voros McCracken mentioned a novel way of looking at the problem, and I thought I’d take a crack at it now that there are no more Carlos Correa free agency articles left to write.
His idea is simple: run linear regressions on team-level AVG, OBP, and SLG and use them to predict run scoring. That’s what we’re all after at the end of the day: runs. Linear regressions are a neat way of approaching this, as I hope you’ll agree when you see the evidence.
First, the data. I took team-level batting statistics and runs scored numbers from the 2010-19 and 2021-22 seasons, excluding 2020 due to its short length. That gave me 360 observations to test. From there, I started regressing. No, I don’t mean I got worse at writing, though I guess you’re the judge of that. I mean that I started to run single- and multi-variable regressions to take a look at the data.
Take batting average, for example. Batting average has a 0.355 r-squared with runs scored. In other words, 35.5% of the variation in runs scored can be explained by batting average. Hey, not bad! That’s a third of the variation. Here’s a graph of predicted runs scored (based on batting average) on the x-axis and actual runs scored on the y-axis:
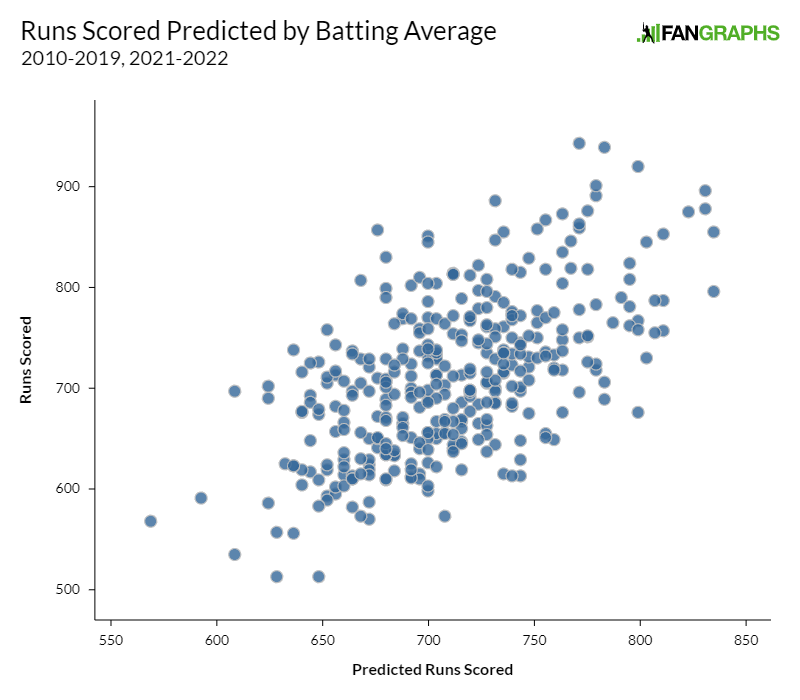
Of course batting average is correlated to run scoring. Aaron Judge batted .311 last year. Austin Hedges batted .163. If your options were no statistics at all or batting average, you’d take batting average every time. But we do have other statistics. On-base percentage, for example, has a 0.668 r-squared with runs scored. That graph looks much nicer:
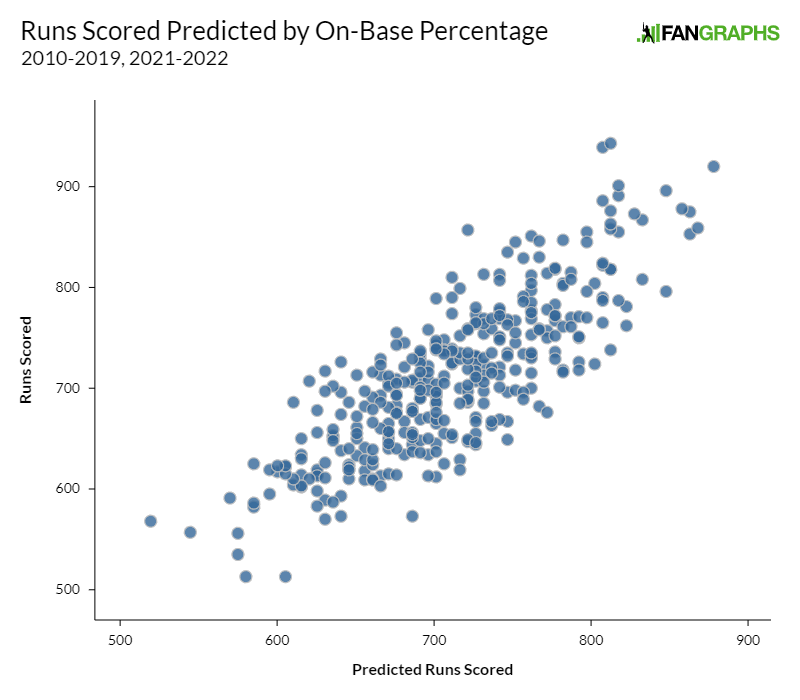
Slugging percentage checks in with a massive 0.84 r-squared, though I’ll spare you the graph on that one. These one-variable regressions make one thing very clear: if you had to judge a player based on only one slash line statistic, average would be at the back of the line.
Being at the back of the line isn’t the same as being useless, so it’s time to press on. If you think regressing against one variable is neat, wait until you hear about multivariate regression. That works basically how you’d expect it to: instead of using one variable to predict runs scored, we can use multiple. For example, if you wanted to predict runs scored using batting average and on-base percentage, you could just chuck those columns into a formula and get what’s called an adjusted r-squared, the percentage of variation in runs scored that can be explained by the combination of average and OBP together. That works out to 0.673 for that combination. If you’ll remember from above, that’s about the same as the correlation between OBP and runs scored. In handy grid form, here’s the r-squared (adjusted for two-variable regressions, raw for single regressions) for each combination of AVG, OBP, and SLG. When a statistic is crossed with itself, that’s simply the single-variable regression:
| Statistic | AVG | OBP | SLG |
|---|---|---|---|
| AVG | .355 | .673 | .841 |
| OBP | .673 | .668 | .885 |
| SLG | .841 | .885 | .840 |
In plain English, if you wanted to predict runs scored with two of the three slash line statistics, you’d choose OBP and SLG. They explain the highest percentage of runs scored. They aren’t perfect, for obvious reasons – they’re summary statistics that ignore sequencing and individual results, they ignore baserunning, and they’re context-neutral – but they still explain nearly 90% of run scoring.
If that’s all I had to show you, I probably wouldn’t have written this article. But there’s a fun little trick I’ve picked up over the years that you can do here. When I created each regression, I also created a prediction for each team-season’s runs scored based on that team’s raw statistics. I also, of course, have their actual runs scored. That means that I have a residual for every data point; in other words, I have the amount that my prediction missed by.
If you’ll remember the top of the article, the question we’re asking is simple: If two hitters have the same on-base percentage and slugging percentage, does it matter if they have different batting averages? The residuals are a great way of explaining that. If batting average is telling us something useful that we can’t get from OBP and SLG alone – in other words, if a .315/.365/.510 line is better or worse than a .260/.365/.510 line when it comes to helping the average team score runs – we should see a correlation between the residual of an OBP/SLG prediction and batting average.
I’ll spare you some suspense – there’s basically no correlation between OBP/SLG residuals and batting average. In other words, OBP and SLG aren’t perfect at predicting runs scored, but their errors can’t be explained by batting average. To stick to the r-squared descriptions I’ve been using throughout the article, only 4.3% of the variation in OBP/SLG residual can be explained by batting average.
For comparison’s sake, I ran the same calculation for each statistic. I took the residual of each two-statistic prediction of runs scored and then saw how correlated those residuals were to the remaining statistic. If you’ll recall from up above, batting average checked in at 4.3%. On-base percentage checks in at more than double, 9.8%. Slugging percentage is even better, at 31.6%.
Hey, you might say. Batting average is half as good as on-base percentage. What’s with all the slander? Bad news, if that was your initial thought: I’ve been holding out on you this entire article. See, I’ve been quoting r-squared as my preferred measure, but r-squared is directionless. It only measures what percentage of variation can be explained by a given variable, not which direction that variation works in. As an example, the r-squared between projected wins and the chances of making the playoffs is high, but so is the r-squared between projected wins and the chances of having the number one pick in the draft. They simply work in opposite directions.
As it turns out, after you predict a team’s runs scored using their OBP and SLG, higher batting average means lower runs scored. If that’s confusing, I’ll try to show it in graphical form. A positive residual means that OBP and SLG under-predicted a team’s actual runs scored. Thus, if higher batting average means more runs scored holding all else equal, you’d expect to see a line from the bottom left to the upper right on the below graph. Instead, as you can see from the superimposed fit line, the opposite is true:
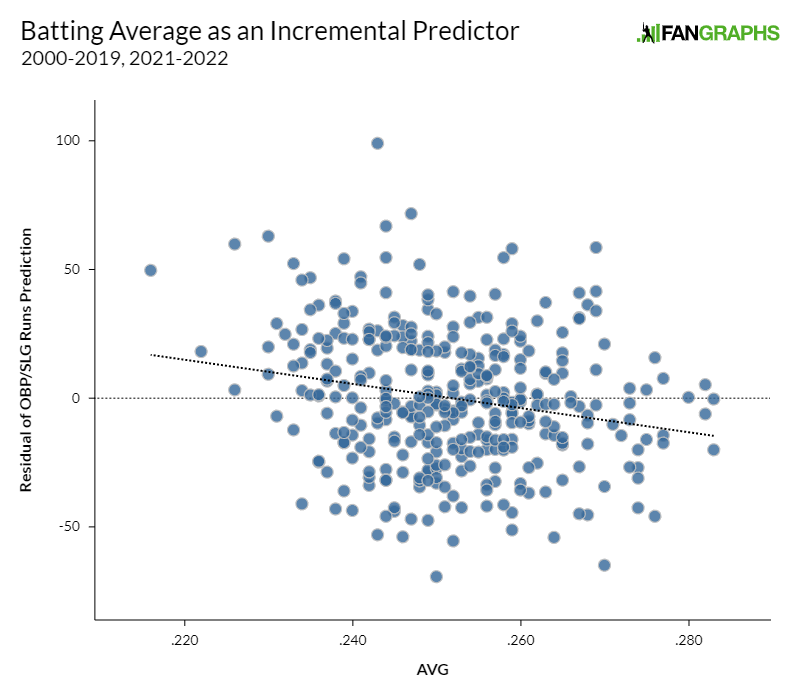
In other words, if you were making a prediction of how many runs a team would score and had only their OBP and SLG handy, you’d do fairly well. But if I whispered that team’s batting average in your ear, you could improve your prediction very slightly. The higher the number I whispered in your ear, the lower you’d revise your estimate. It wouldn’t be by much – there’s almost no useful predictive power in batting average – but to the extent that you moved your estimate, it’d be in an unintuitive direction. If you know a team’s OBP and SLG, batting average gives you very little additional predictive power, essentially noise in a weird direction.
That’s very likely an artifact of my dataset, but think of it this way: in terms of the magnitude of the effect we’re looking for, batting average is swamped by the other two statistics. I ran a multivariate regression with all three slash line statistics to illustrate this. For every 10 point increase in OBP, a regression predicts 28 more runs scored in a full season. For every 10 point increase in slugging percentage, it predicts 20 more runs. For every 10 point increase in batting average, it predicts 12.5 fewer runs, with much larger error bars than the other two. The combined adjusted r-squared of the three-variable regression is 89.8%, basically indistinguishable from the 88.5% you get from OBP and SLG.
This is a lot of words about a topic that’s already been settled, but I think it’s worthwhile to belabor the point. The modern view that OBP and SLG are more important than batting average for scoring runs isn’t opinion or preference. It’s borne out by the way that real teams score real runs in real games. Batting average is better than nothing, but it’s meaningfully worse than the other statistics we have available, and adds no useful information if you already know OBP and SLG. Unless you’re playing fantasy baseball, you can safely skip over average when you’re looking at how valuable a player was offensively. Don’t take my word for it – that’s just what happens when they play the games.
Ben is a writer at FanGraphs. He can be found on Bluesky @benclemens.

ISO has entered the chat
Need a similar stat for OBP minus AVG.
For most players the difference between AVG and OBP is walks.
For qualified batters in 2022, BB% and OBP-AVG has a 0.95 correlation, so I’d say if you need that, just look at BB%
If you’re Mark Canha or Brandon Nimmo, hit-by-pitch is also a significant component of OBP.
That exists and is used, but as rosen notes, it’s basically just walk rate these days. Nobody’s sac bunting anymore, and sac flies are generally rare. Only 3 guys reached 10 SF last season and only 10 hitters even got to 8.