Using the Value of Taking Pitches to Describe Different Hitter Approaches
I will never not be fascinated by the fact that hitters actually produce negative value when swinging. In my most recent article outlining the struggles of Jarred Kelenic, I briefly discussed this idea. Even in a sea of hitters who are below-average when swinging, Kelenic stands out as being particularly bad when he takes a hack; he’s been worth roughly -6 runs per 100 swings so far this year. And as I noted, the hitters who do the best at limiting the damage on their swings tend to be baseball’s most productive hitters overall. From that research, I found an R-squared of 0.714 between a hitter’s run value when swinging and their seasonal wOBA.
That makes a ton of sense: Hitters who maximize their production on swings — that is, both limiting whiffs and making frequent loud contact — tend to be better hitters overall. But this also got me thinking about the reverse: How does taking pitches influence a hitter’s overall production? From the Kelenic research, I found only a moderate correlation between take value and seasonal wOBA, with an R of 0.422 and an R-squared of 0.178. That’s not to say that better “takers” aren’t better hitters; it just suggests that having extremely high-value takes doesn’t necessarily lend itself to having more success overall. For posterity’s sake, here’s the plot of 2021 hitters’ run value per 100 takes and their seasonal wOBAs. Players on both ends of the wOBA spectrum are highlighted just to demonstrate a few individual examples:
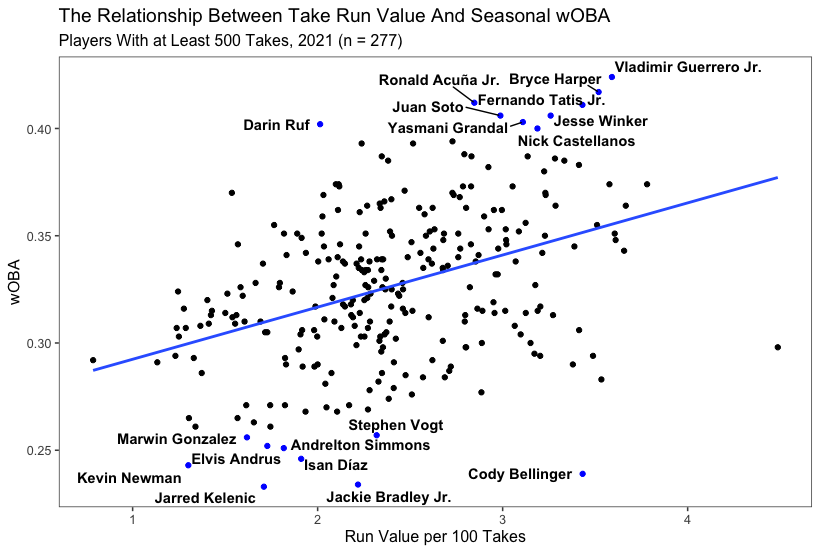
There is definitely a relationship there, but it’s not that strong. Cody Bellinger, for example, is having a pretty awful season, and a lot of it has to do with what happens when he does make contact. His .336 xwOBA on contact is almost 30 points below the major league-average, and it’s roughly 150 points below his 2019 figure, when he won the NL MVP. That, combined with the fact that he’s whiffing on nearly 30% of swings, has led to the 49 wRC+. And yet Bellinger has a shade more take value than Fernando Tatis Jr., who is in the running for the NL MVP this year with his 158 wRC+ and 5.1 WAR. For him, the contact quality has been on the other end of the scale, highlighted by a .550 xwOBA on contact. And though Tatis does whiff at very high rates, it hasn’t mattered because the quality of contact is so good.
These two examples are meant to provide evidence for what you see in the plot: You can be good at taking pitches, but that doesn’t guarantee success. Minimizing whiffs, producing loud contact, or some combination of both is much more important. But that still doesn’t explain a couple of important questions. For instance, why are some hitters better at taking pitches than others? And even if it doesn’t explain overall top-line success, are there are other outcomes that are more highly associated with being good at taking pitches than wOBA?
First, let’s consider what run value actually means. It’s based on a run expectancy matrix known as RE288, the run expectancy for the 24 base-out states across each of the 12 count states. Effectively, taking a ball on a 3–2 count is more valuable than taking a ball on an 0–2 count. In the former scenario, you’ve drawn a walk. In the latter, you’ve dug yourself out of the deepest hole, but hitters’ numbers 1–2 aren’t that much better anyway. The incremental ball probably won’t mean much.
There’s a fairly strong correlation between take run value and the proportion of takes that are balls, but since so much of this is count dependent, there’s still a lot of unexplained variation. The R-squared for this association is 0.665. You can see the relationship plotted here, with large residuals plotted in blue:
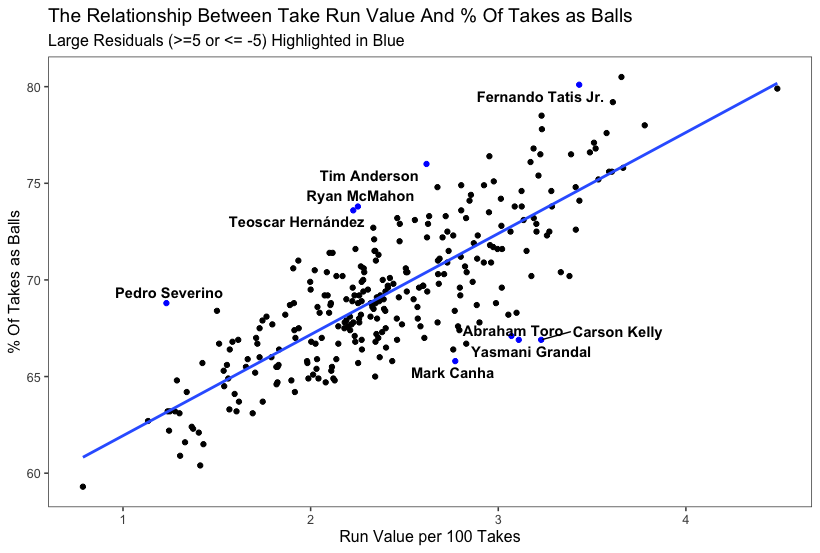
This provides valuable insights into each hitter’s approach, with the residuals providing the important details. Look at Tatis again. More than 80% of his takes are at balls, the second-highest rate in baseball. But why is his residual so high? It’s because these takes typically come in two-strike counts: of Tatis’ 851 takes this season, 225 have come in two-strike counts. His 26.4% rate is in the 88th percentile. Luckily for him, though, with more than 80% his takes coming at balls, he’s actually avoiding a ton of strikeouts in the process. That’s a different spin on plate discipline than we might typically think about, with a focus on raw walk and strikeout numbers and not so much on strikeouts avoided. The opposite is happening for someone like Grandal, with just under 20% of his takes coming in two-strike counts. He leads baseball with 39% of his takes this season coming while ahead, a staple of his high-walk, high-strikeout, loud-contact approach that has yielded a .228 batting average, but a 161 wRC+ thanks to his 24% walk rate and .301 ISO.
In short, hitters above the line take more balls, but these are coming in less advantageous spots. Hitters below the line may take fewer balls, but their takes are inherently more valuable compared to the expectation. Tatis takes a ton of balls, but each of these takes matters less in terms of run expectancy if they’re coming in worse counts. Grandal, on the other hand, takes almost everything — meaning that he’ll also be taking quite a few strikes — but these takes ultimately lead to a lot of walks, as demonstrated by their higher total value than otherwise expected for that take-ball rate.
Beyond the Tatis and Grandal examples, we can see how the high and low residual players differentiate when they take. I would describe the players in the “high residual” category as “defensive takers,” those who take more pitches when behind in the count. Those in the “low residual” category, on the flip side, would be “offensive takers,” with more of their takes coming in hitter’s counts. Here’s the proportion of takes for each group, sorted by the largest differences between the groups (low residual — high residual):
| Count | High Residual | Low Residual | Difference |
|---|---|---|---|
| 1-0 | 9.2 | 11.7 | 2.5 |
| 2-0 | 3.0 | 4.8 | 1.8 |
| 3-1 | 1.4 | 2.9 | 1.5 |
| 2-1 | 4.0 | 5.3 | 1.3 |
| 3-0 | 1.6 | 2.3 | 0.7 |
| 3-2 | 2.7 | 3.4 | 0.7 |
| 0-0 | 31.8 | 32.4 | 0.6 |
| 1-1 | 9.2 | 8.9 | -0.3 |
| 2-2 | 6.8 | 5.2 | -1.6 |
| 0-1 | 13.0 | 11.2 | -1.8 |
| 0-2 | 7.5 | 5.1 | -2.4 |
| 1-2 | 9.6 | 6.7 | -2.9 |
We can simplify this further by just focusing on count classifications: batter ahead, even count, batter behind, two strikes, and three balls:
| Count | High Residual | Low Residual | Difference |
|---|---|---|---|
| Batter Ahead | 22.0 | 30.4 | 8.4 |
| Even Count | 47.9 | 46.6 | -1.3 |
| Batter Behind | 30.2 | 23.0 | -7.2 |
| Two Strikes | 26.6 | 20.4 | -6.2 |
| Three Balls | 5.7 | 8.6 | 2.9 |
This is the clearest way to see how the two groups of players differ. Again, the low residual players take more while ahead, while the high residual players take more while behind. Thus, the residual can be used as a simple proxy for a hitter’s overall approach, and actually correlates moderately well (R of -0.480, R-squared of 0.231) with a hitter’s walk-to-strikeout ratio:
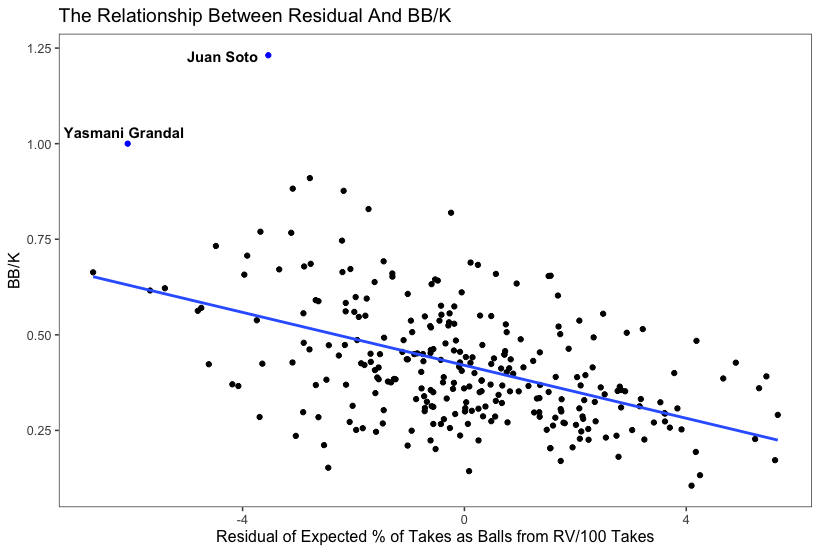
As you can see from this relationship, as a hitter’s residual decreases — as they become a more “offensive” taker — their walk-to-strikeout ratio increases. On the flip side, as a hitter’s residual increases, and they become a more “defensive” taker, they are more likely to post worse walk-to-strikeout numbers.
What does all of this tell us? Well, take run value on its own doesn’t give us that much information. But when we unpack where take value comes from — and adjust for each hitter’s proportion of takes as balls — we can better understand different approaches for different batters. And while it may not perfectly explain the hitter’s top-line walk and strikeout numbers, it provides a key indication as to how differing approaches interact with these types of discipline-driven results.
Devan Fink is a Contributor at FanGraphs. You can follow him on Twitter @DevanFink.

Excellent article and I appreciate the insight! Who are the two unlabeled outlier dots on the upper two graphs (right bottom-ish on the first graph, very top right on the second)?
Also curious who that is on the bottom left on the second graph. 🙂
Bottom left is David Fletcher, at 0.79 runs above-average per 100 takes
That would be Jeff McNeil, who has been worth 4.49 runs above-average per 100 takes this season.