Andrés Muñoz Is an Analytical Blind Spot

If you are familiar with Andrés Muñoz, the baseball player, you may know that he is good. It may be enough for you to simply witness and bask in his elite performance, and question it no further. (Rarely are we so content here.) You may not realize he is unusual; you may not care. Often in baseball, being good and being unusual go hand in hand. This is a short exploration, albeit one preceded by an exorbitantly long prologue, of why Muñoz is good and unusual.

If you are familiar with FanGraphs, the baseball website, you may know about approach angles. If not: A pitch’s approach angle is the three-dimensional angle at which it crosses the front of home plate. Broken down into its two-dimensional vectors, it becomes vertical approach angle (VAA) and horizontal approach angle (HAA).

VAA is a description of pitch shape and thus depends on other physical attributes of the pitch — namely, its velocity and acceleration in all three dimensions. While representing the most distilled measurements of a pitch’s movement through space, the velocity and acceleration vectors themselves are functions of release height, release angle, release speed, spin rate, spin axis, spin efficiency… it goes on. VAA, as it happens, is very sensitive to pitch height. Reporting a pitch’s average VAA is not especially meaningful without either providing locational context or stripping it of that context all together.

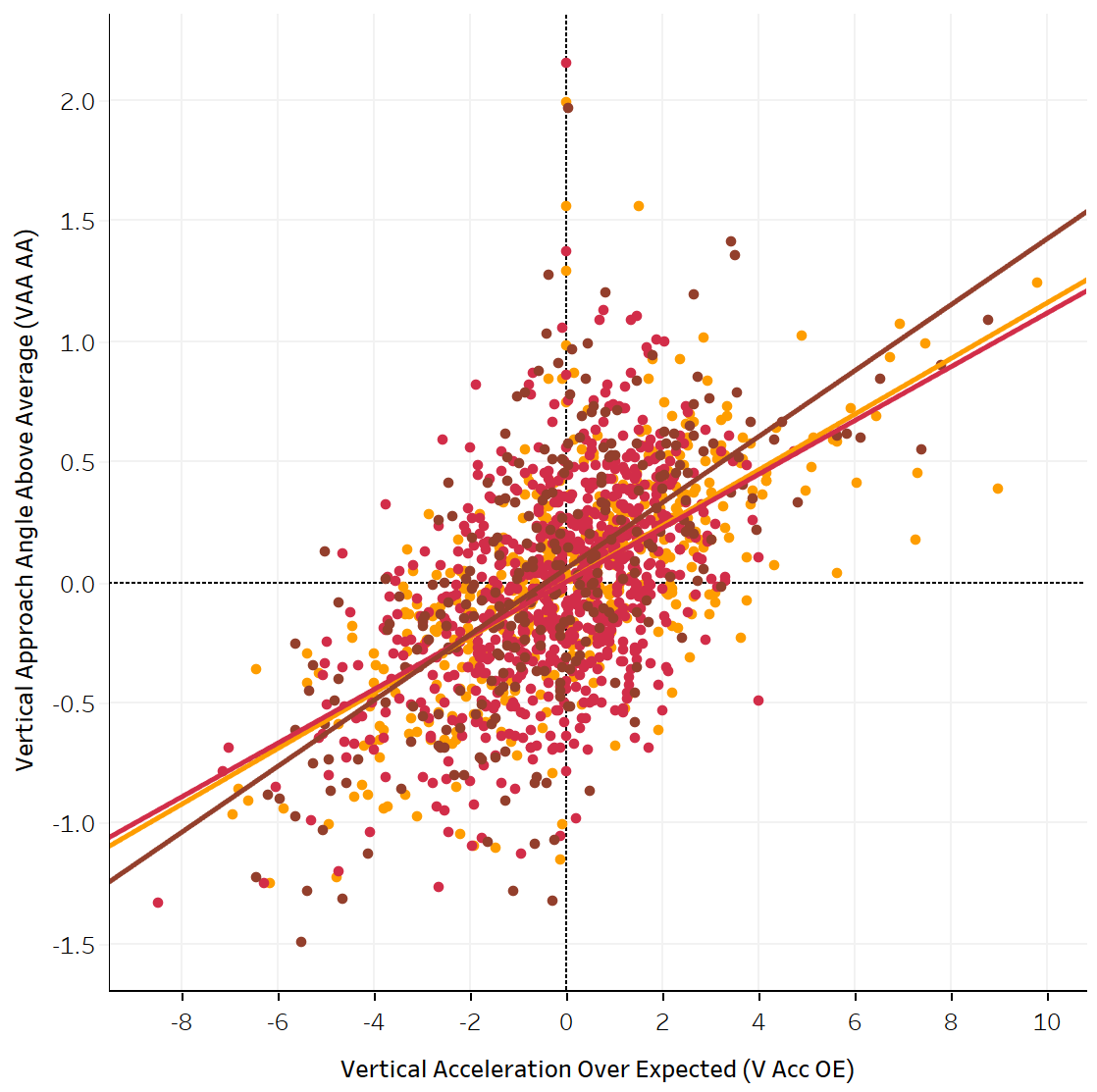
To accomplish the latter, I developed VAA Above Average. It’s a simple recalculation that communicates a fastball’s flatness or steepness irrespective of pitch height. Through this it’s much easier to see that, for example, flatter VAAs induce higher swinging strike rates (SwStr%) at all pitch heights compared to steeper VAAs (forgive the half-baked visualization):

VAA and VAA Above Average have proven helpful in explaining why guys with atypical characteristics — for example, low-slot, low-velo pitchers such as Paul Sewald and Joe Ryan — can cultivate success despite conventional indicators portending otherwise. But VAA Above Average, like VAA, is just a measurement, a descriptor. VAA AA can correlate with performance and/or expectations — I’ll get to that — but the metric itself was never intended to make any declaration about expectations, specifically the opposing hitter’s expectations, upon which so much of pitching success is predicated.

That, rather, would be the job of the dead zone. The term “dead zone” typically describes unspectacular movement traits that yield poor outcomes. The farther a pitcher’s movement traits from the dead zone, the better his fastball is assumed to be. In its infancy, public-side research misunderstood the dead zone to be singular, a fixed set of movement traits all fastballs should avoid. Now, it’s much better understood, at least among those of us who care unnecessarily deeply about it, that this is not true: The dead zone is a function of induced vertical break (IVB), also known as “ride” or “carry.” And IVB, very crucially, is a function of arm angle.

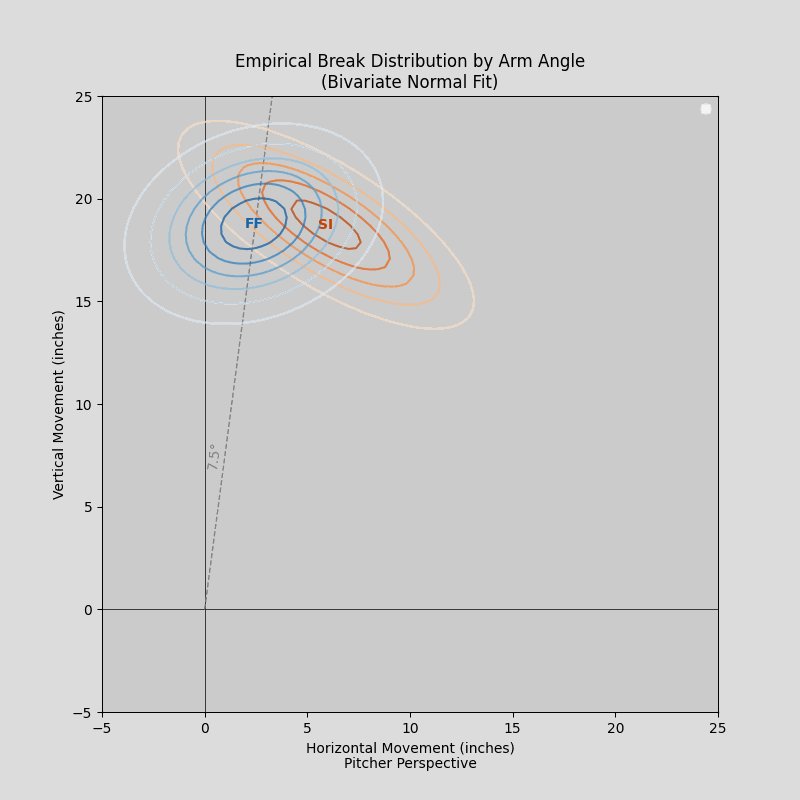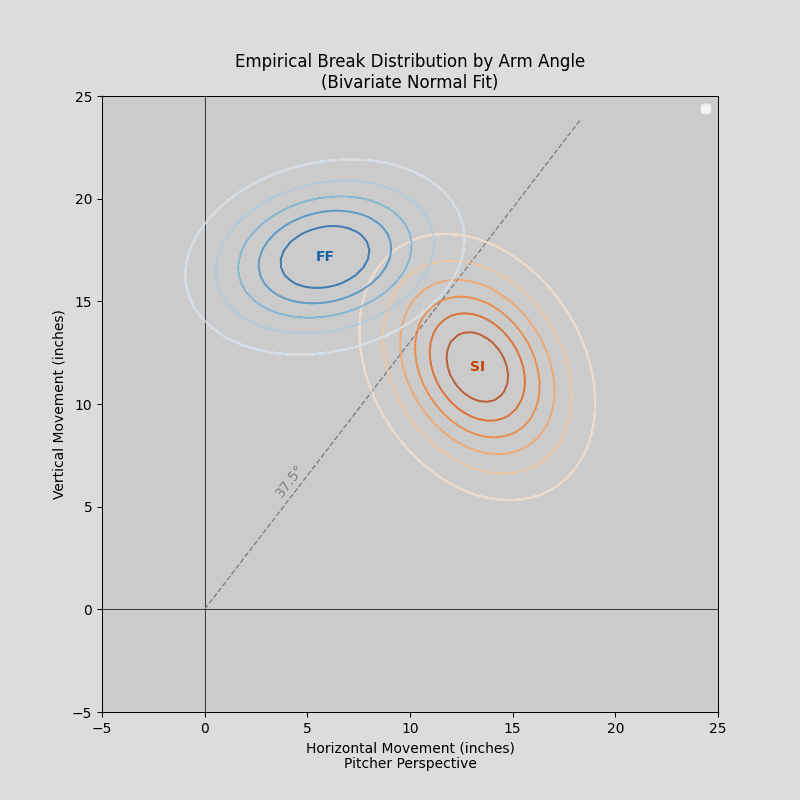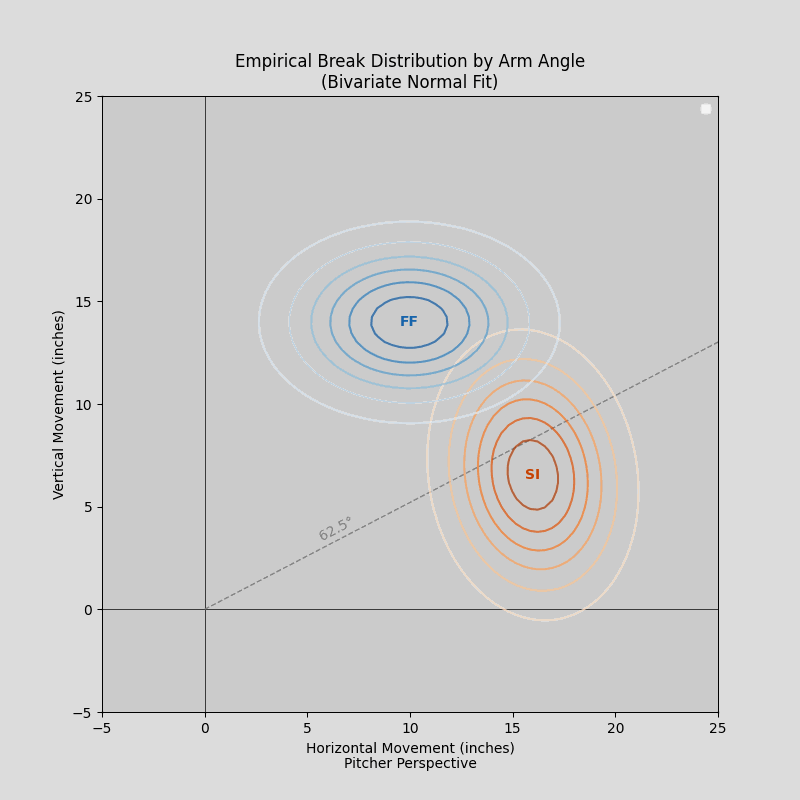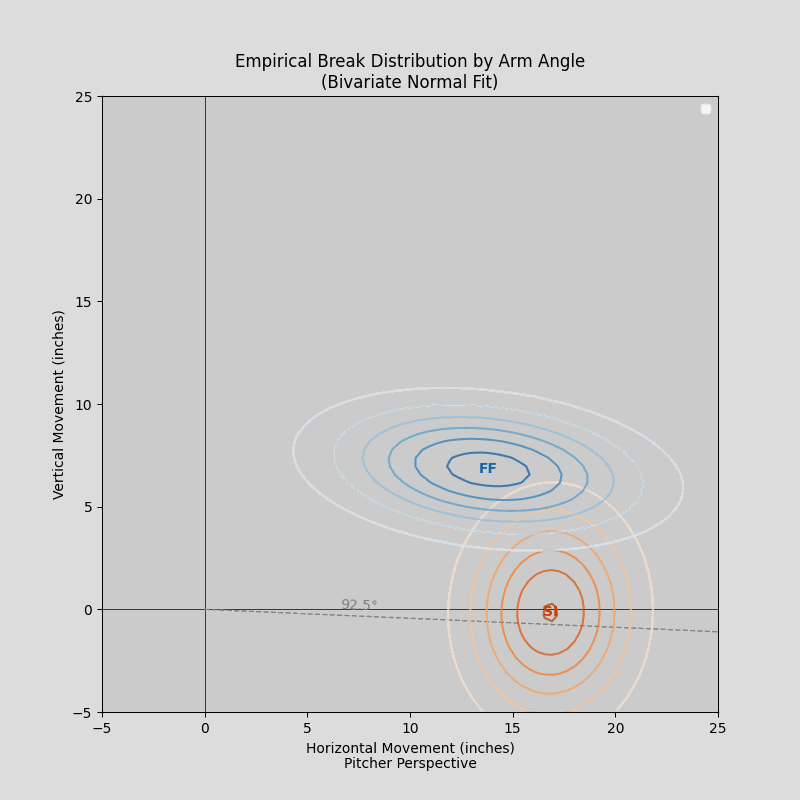
Courtesy of Max Bay’s Streamlit app

Higher-slot pitchers will naturally generate more IVB than their lower-slot counterparts. Even a flame-throwing side-armer may generate less IVB than someone throwing more softly from directly over the top. To claim the former’s fastball is worse than the latter’s on the basis of IVB alone is analytical malpractice.

If one were to weaponize the transitive property for personal gain, as I will do here, one might correctly assert (1) if IVB is a function of arm angle and (2) the dead zone is a function of IVB, then (3) the dead zone must also be a function of arm angle. This brings us to the dynamic dead zone (DDZ). DDZ still presumes that a pitcher’s fastball’s performance improves with more distance from the dead zone, but now a unique dead zone is custom-fit to each pitcher. Until very recently, it had not been estimated on a pitch(er)-by-pitch(er) basis and curated for public analytical use.

Max Bay, who now works in R&D for the Dodgers, developed a Streamlit app that models and visualizes DDZ:

For any given pitch type, we model the release characteristics—arm angle d and pitcher height-scaled extension e—along with pitch acceleration components (a_x, a_z) jointly as a 4-dimensional multivariate normal distribution.

The rest of his explanation is enough to pulverize your brain. Bay’s app not only models the DDZ for every pitcher and his fastball(s) but also shows the delta between what’s observed (i.e., actual movement) and what’s expected (the DDZ). A positive delta indicates more vertical movement than expected while a negative delta means less. (Note that negative does not mean bad; magnitude trumps directionality.) Take, for example, Mason Miller, circa 2024, whose four-seamer ranked second in Stuff+ among qualified relievers who threw their four-seamers more than 2% of the time:

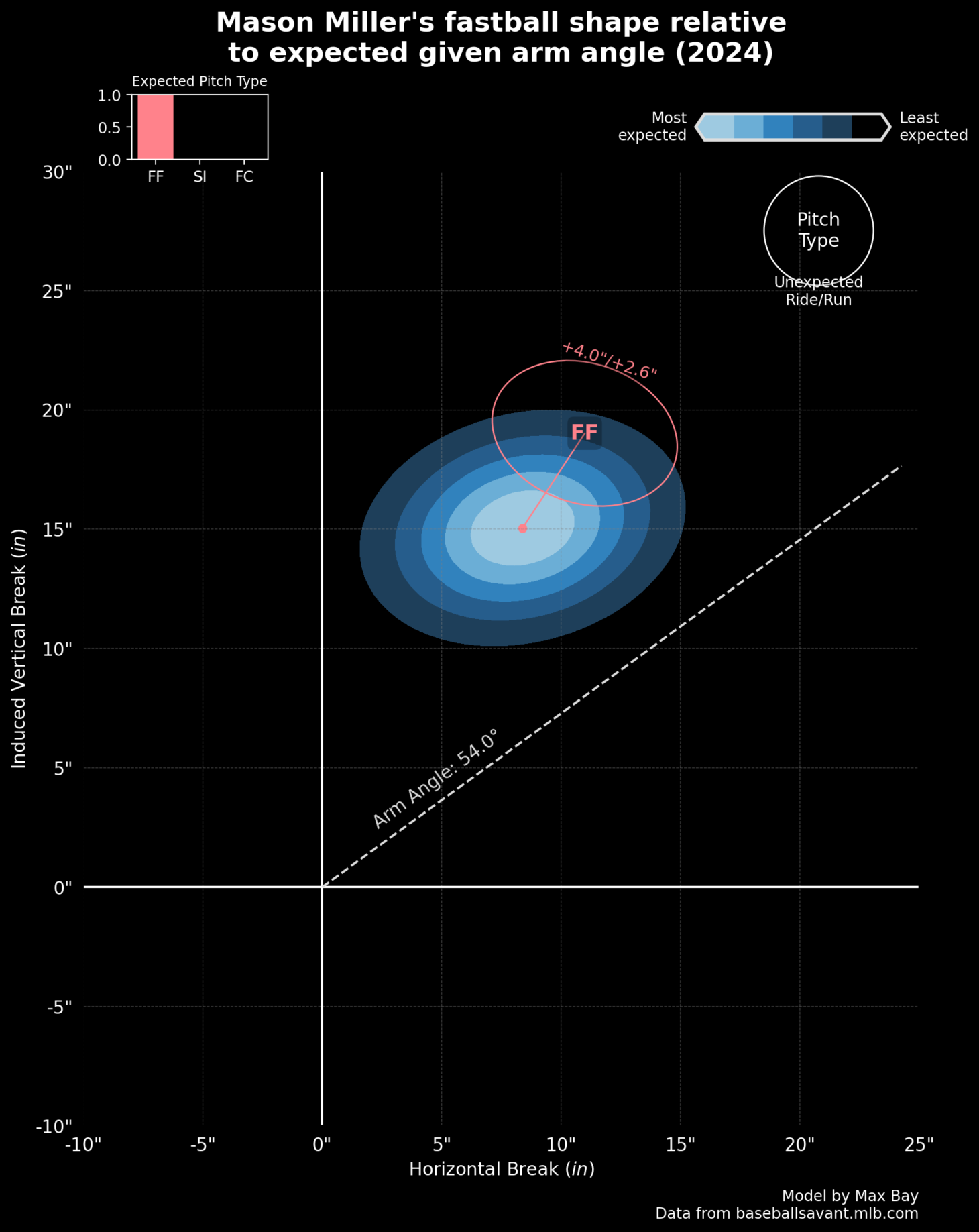
…versus Luis Severino, circa 2023, who pitched to a 6.65 ERA that year:

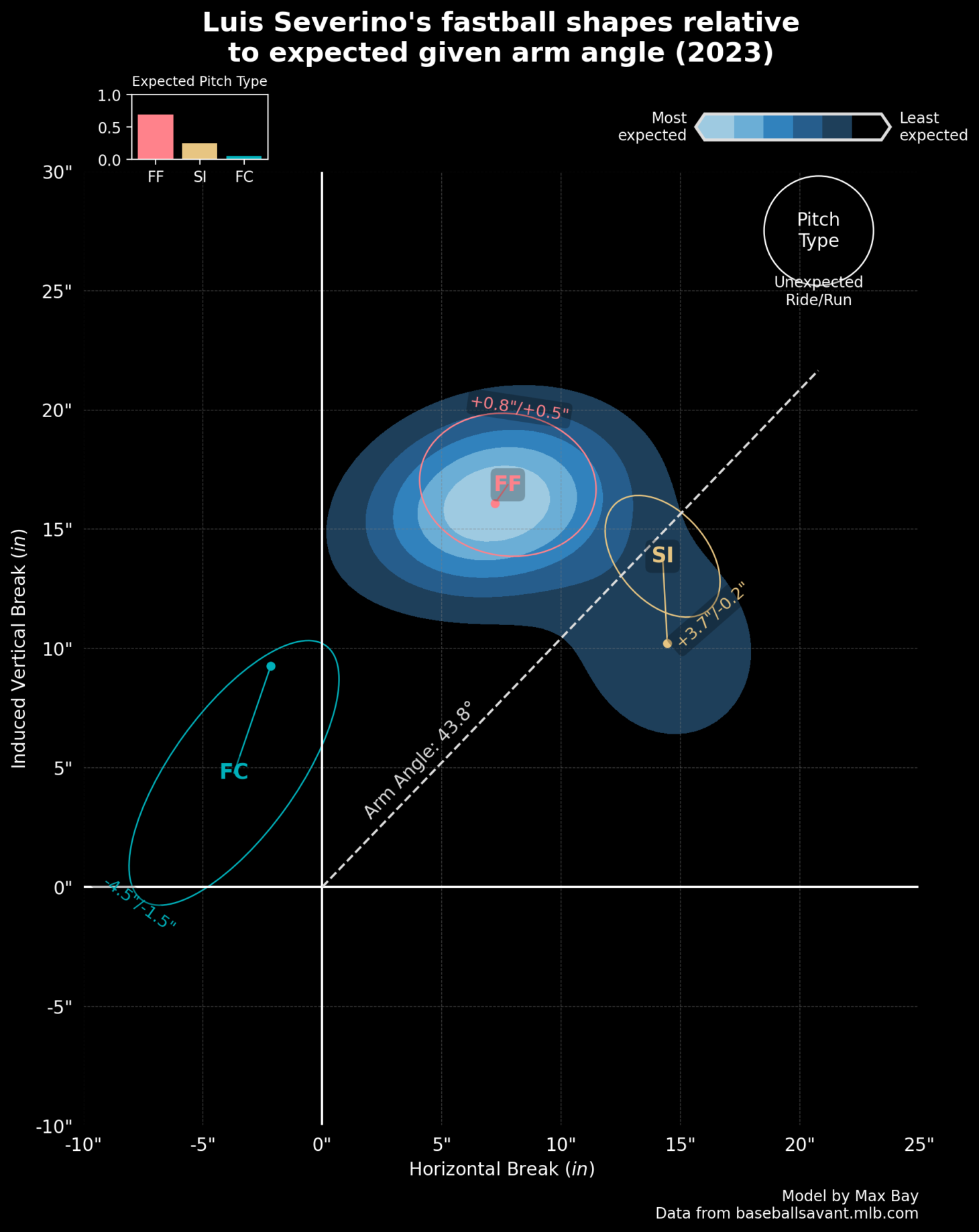
A fastball’s vertical DDZ delta and its VAA Above Average can be very similar on their faces. They are both functions of vertical acceleration and thus naturally correlate with each other. But they are neither identical nor substitutable; as noted, one is just a measurement while the other is a concerted effort to characterize hitter expectations. In conjunction with each other, they tell a variety of different stories about fastball shapes: above-average flatness (high VAA AA) but ordinary shape (nonexistent DDZ delta); ordinary flatness (zero VAA AA) but unusual shape (robust DDZ delta); even something like flat VAAs but negative IVB expectations; and so on and so forth:

(For reasons presently unknown to me, the relationship between the DDZ delta and VAA Above Average is much weaker for four-seamers [r-squared = 0.23] than for sinkers [r-squared = 0.42] or cutters [r-squared = 0.39]. It could be a pitch classification thing, it could be a trait unique to four-seamers that allows for much wider variation in their pitch designs and shapes — I don’t know. That’s neither here nor there at the moment. A question for another day.)

What does Muñoz have to do with any of this? His four-seamer is flatter than average per VAA Above Average (+0.59 degrees, as of May 4) but is very nearly a dead-zone fastball (+0.2 ft/sec squared), per my DDZ delta calculations. For posterity/reference, here are Muñoz’s DDZ and deltas from 2024:

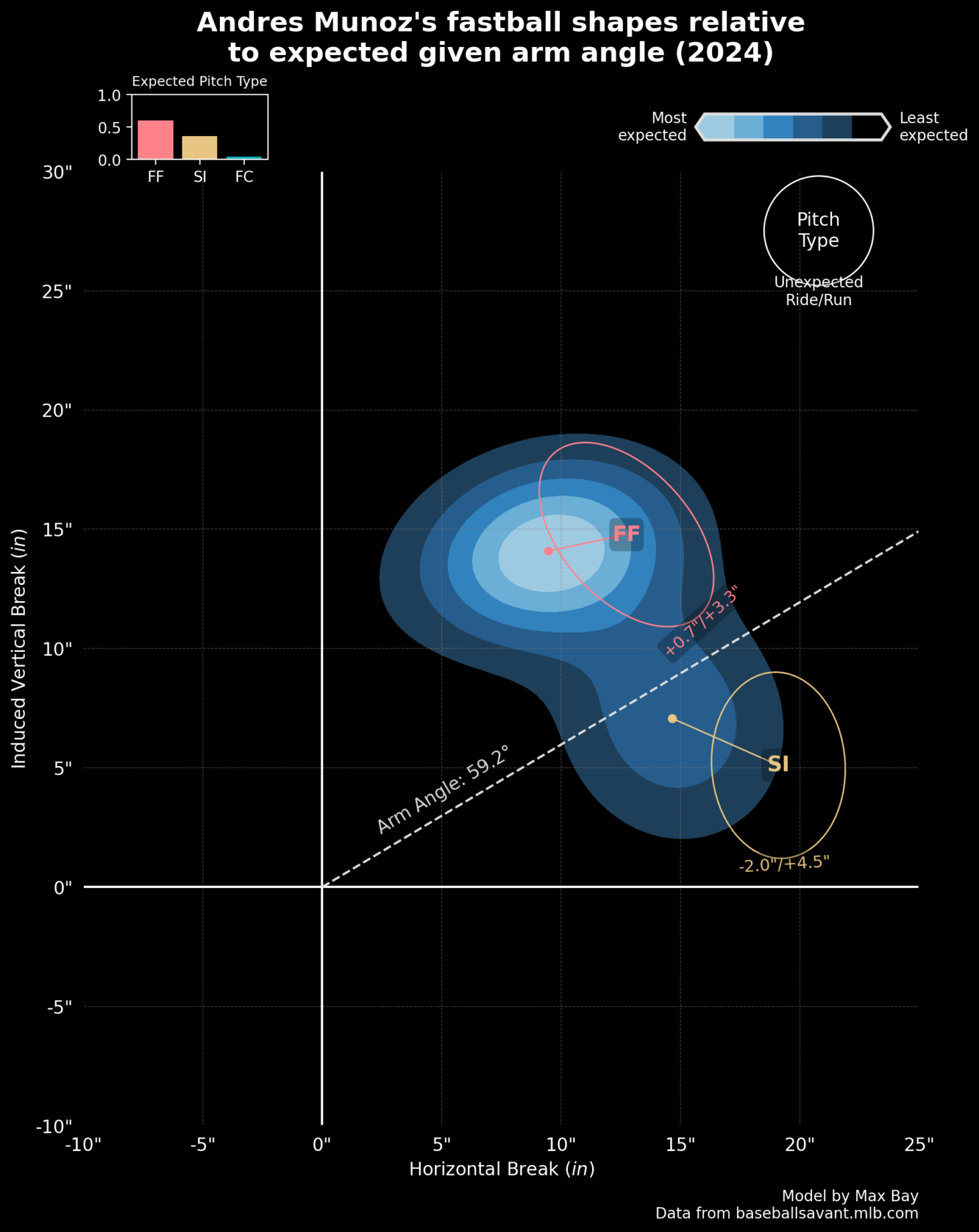
A guy possibly named Ed asked me: Despite its flatness, how does Muñoz’s four-seamer induce so many groundballs — results typically associated with steep four-seamers, not flat ones? Moreover, if it’s truly a dead-zone fastball, how does it succeed at all?

Bay models DDZ using the acceleration vectors parallel to the strike zone — what we could consider north-south and east-west — and specifically not the acceleration vector in the direction of home plate from the pitcher’s mound (a_y, which is the acceleration vector informed by release speed). As Bay notes in his app, “I use release-direction-relative acceleration as the operant metric for shape because it is independent of time under a constant acceleration model, and I did not want time to plate as a source of variance.” Despite this notion, we can see how vertical DDZ deltas for four-seamers are sensitive to pitch velocity and vary dramatically when juxtaposed with arm angle:

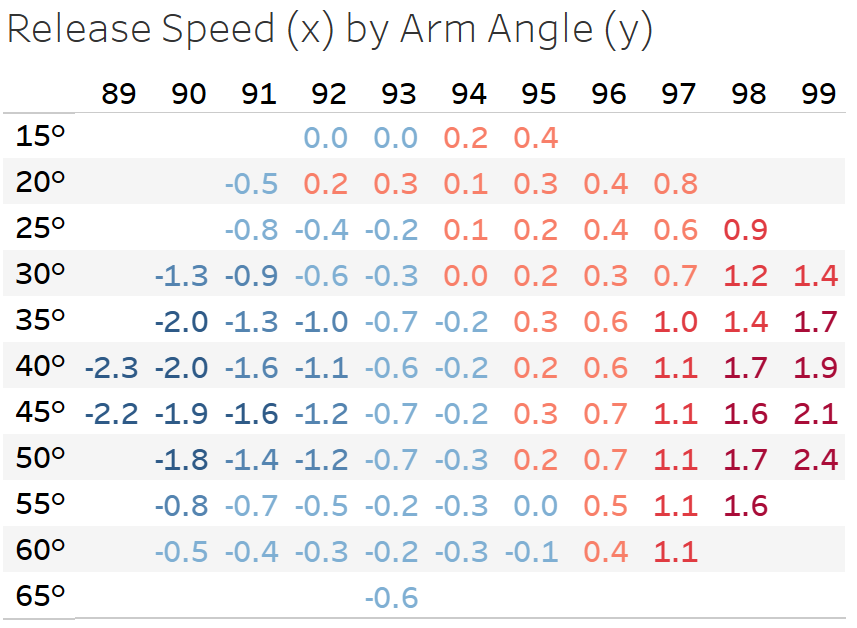
In the table above, Muñoz’s four-seamer typically inhabits the space of 98–99 mph and 25–30 degrees, where the average DDZ delta is somewhere between +0.8 to +1.4 ft/sec squared. Yet his actual delta, at +0.2 ft/sec squared, would be noticeably lower if his dead zone were to account for this. In other words, a dead zone also conditioned on velocity would set an expectation of more IVB than he actually creates, not less. This would result in a directionally negative delta — and that would better reconcile with his unusual groundball tendencies because it implies that hitters, expecting more ride based on his velocity, swing over the top of his fastball and drive it into the ground.

When Bay originally modeled DDZ, he incorporated arm angle and height-scaled extension because arm angle, height, and extension are all physical attributes that a hitter can immediately and reliably ascertain visually. Everything else that affects movement — spin axis, seam orientation, etc. — can be picked up, for sure, but not consistently or with certainty. This distinction is important.

On this theoretical basis, velocity is in purgatory. Is velocity something a hitter can visually and mentally reconcile? Of course. A hitter can pick up a pitcher’s velo through prior encounters, live looks, even video scouting — and he can make those subconscious connections rather quickly. But can he do so with certitude? I’m not so sure (and neither is Bay). Pitch selection prevents that, for one; the hitter can’t know, resolutely, what will be the next pitch thrown. Even if a pitcher throws only fastballs, there is arguably enough variance in velocity from one pitch to the next that the hitter’s timing-up of the fastball is never a sure thing. A hitter doesn’t need to know a pitcher’s exact arm angle — an approximation will do, and any between-pitch variance in the arm angle will likely be undetectable anyway — but a hitter has to have the velocity absolutely nailed down to succeed. Moreover, from a modeling standpoint, higher velocity yields more acceleration in all dimensions, such that the x- and z-plate accelerations already have a signal for release speed baked into them.

Given all this, it makes sense not to model velocity as a dimension of the dead zone. Still, I went ahead and did the thing Bay warned against and introduced time to the plate (to capture the interaction of release speed and extension) into the DDZ calculations, then assessed if the new deltas better correlated with performance. For my performance variable, I used “launch angle influence,” which is basically launch angle controlled for pitch location and each opposing hitter’s swing decision and launch angle tendencies (in the absence of bat angle, swing path, or other swing measurements that inform a hitter’s launch angles). Ideally, a fastball’s launch angles would be directionally consistent with its delta: lower launch angles for negative deltas as hitters swing over the fastball, higher launch angles for positive deltas as hitters swing under it. Obviously, launch angles alone do not make or break a pitcher, but it is a metric whose directionality and magnitude can serve as a strong signal for us.

I liked what I found: Four-seamers thrown 500 times since the start of 2024 (n = 218) correlated better with launch angle influence when the dead zone and its ensuring deltas account for velocity (r-squared = 0.36) compared to not (r-squared = 0.26). The same can’t quite be said of sinkers (r-squared = 0.34 before, 0.38 after), and it’s a wash for cutters (r-squared = 0.00 before, 0.06 after), mostly due to small sample issues. Muñoz’s deltas, specifically, shifted from +0.5 ft/sec squared to -0.4 ft/sec squared in 2024 and +0.2 ft/sec squared to -0.2 ft/sec squared in 2025 (+0.4 ft/sec squared to -0.3 ft/sec squared in aggregate). It’s not a huge change — other pitchers incurred significantly larger ones than Muñoz did — nor does this change come close to explaining all of Muñoz’s success. But it’s a change in what I would expect to be the correct direction, and, again, directionality is key here.

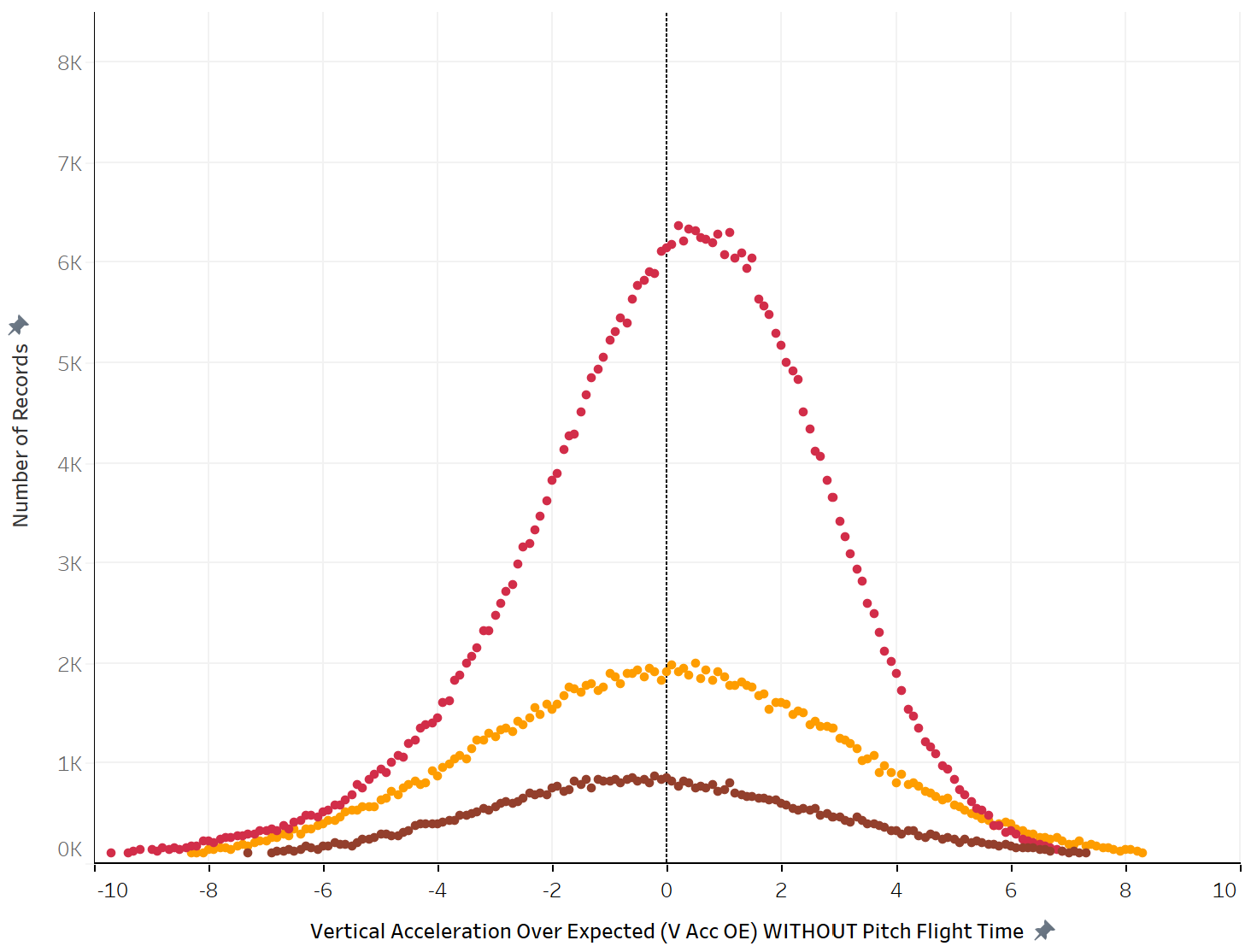
If nothing else, the distribution of DDZ deltas tightens after including velocity. Before:

After:

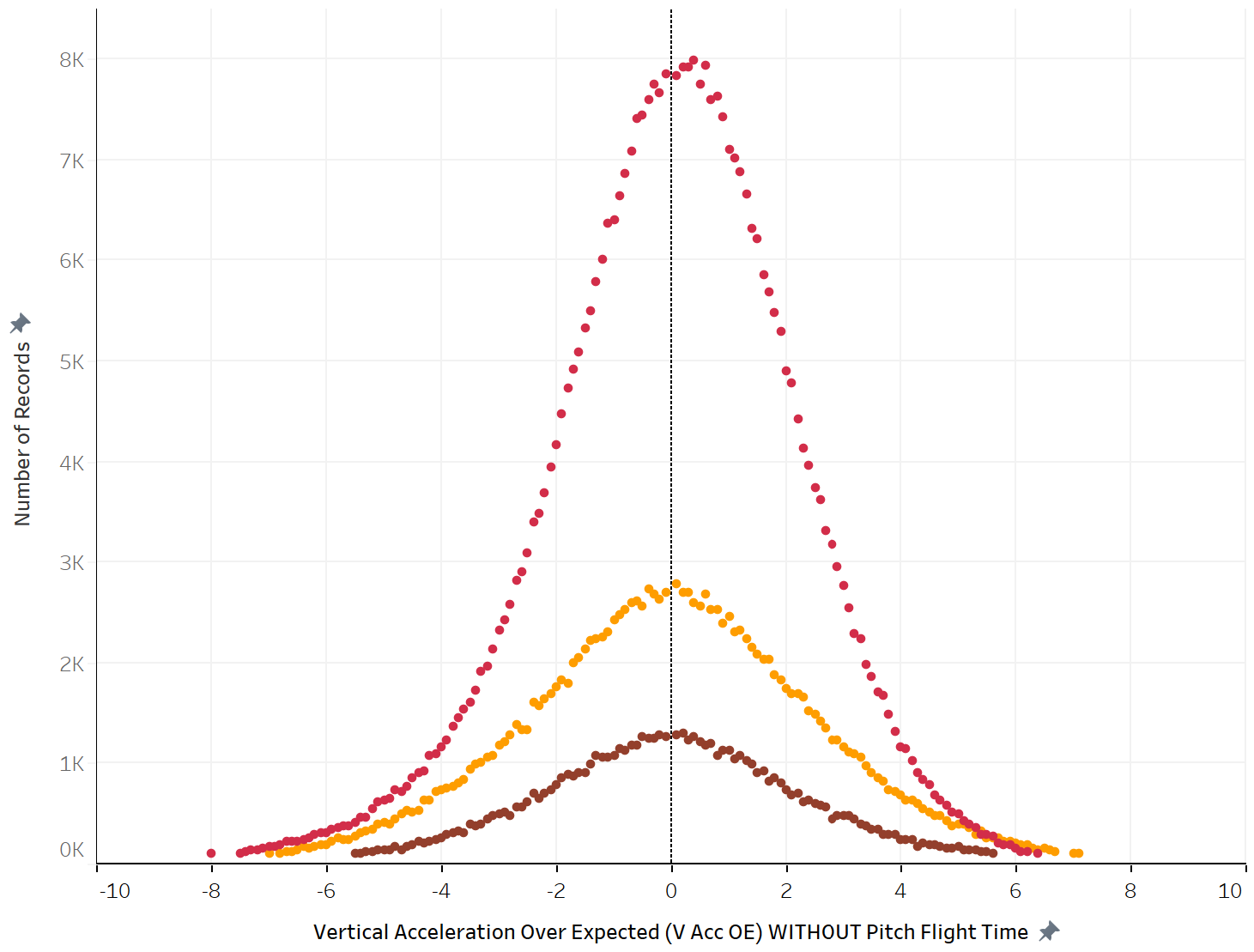
So, does velocity help set a hitter’s expectation for fastball movement? I don’t have a horse in this race, nor am I even fully convinced I’ve done this with sufficient rigor. But I do think there’s enough of a bread crumb here to convince me it’s a possibility, even if only for four-seamers. I need someone smarter than me — Bay, preferably, but he has departed the public sphere — to validate and explore the idea. Maybe that’s you, my potentially capable reader. Until then, we depart on a cliffhanger.

Resources

Bay’s DDZ Streamlit app has not been updated since his tenure with the Dodgers began. I am not half as capable as he is, but I have tried to faithfully recreate his dead zone metrics and provide them publicly on the “Shape” tab of my Pitch Leaderboard. You can cross-reference my numbers from 2024 and prior to his app; they tend to be very close but not exact. (Much of this discrepancy is, I think, attributable to my omission of height-scaled extension, and I also currently separate righties from lefties rather than lump everyone together.) As such, I feel fairly confident in the accuracy of the calculations for 2025. If you have questions, concerns, musings, whatever about DDZ deltas, let’s hear ’em — although I admit I may not be the best person to ask.